2024, Week 1

The year begins auspiciously with books, music, an elusive castle and mathematics. On New Year’s Day I finish reading Farid ud-Din Attar’s The Conference of the Birds. Read long ago, I was prompted to re-read by the fact that in the book, a prominent role is played by the hoopie bird, the bird that is the crest of the Reloading coat of arms (see De re juridica). Although the work is a tour de force and there is much wisdom in its pages and I am not opposed to mysticism per se, Sufism is not for me. In Sufism, the aim is to seek God through dissolving the self and its precepts. These latter include the world which is but a shadow of God. A shadow whose only purpose is to serve as an opposite to the divine light that is sought. The world and all its beauty, mystery and complexity is meaningless and it is with this that I have a problem. It is further unclear whether, on the intricate and strange paths that lead to God, one is supposed to help others or to pursue God alone, ignoring all else.

Reading Kohei Saito’s Capital/Marx in the Anthropocene, Towards the Idea of De-growth Communism, I find a very different view. For Saito, the world is a system whose mode of operation has been upset by capitalism. If humanity is to have a future, we must find a way of pursuing our ends without upsetting the system. Unlike the Sufi Attar, Saito sees the world as something that has meaning and value. It is our purpose to understand and respect the workings of the world so that we may learn how to live in accord with it. This is the ethos of Reloading Humanism and both theoretically and with respect to concrete proposals, I see Saito’s book as a breakthrough. Offering a new evaluation of Marx, Saito sees the later work of the philosopher/economist as having been specifically concerned with precisely the problems that we face today. In solving our problems, where Ulrike Herrmann suggests a top-down, centralist approach (see the Ulrike Herrmann article on the Reloading Humanism People Page), Saito proposes an bottom-up approach. In general, Saito and Hermann agree on the main points of their analyses and both conclude that the only option available to us is de-growth. Although differing on how this is to be achieved, their suggestions are not necessarily mutually exclusive. In Europe, complementing the Fearless Cities and other such initiatives cited by Saito, there are the centralist measures introduced by the EU. Supplying sketches of an answer that I had doubted whether it would ever come, in the wake of reading Saito’s book, on the Reloading Humanism People Page, I summarise his views towards the end of the Ulrike Herrmann article. I also adjust the statement made on the Mission Page, making it clear that what was hoped for, has now been found. Soi-e-a-o-u! Soi-e-a-o-u! (for the origins of this life affirming exclamation see 2023, Week 23).
2024, Week 2
Apart from repeatedly refining the summary of Saito’s book, I also work on the Dürnstein audio guide and find out that up on the hill above the town, there was once a second defensive structure. Known as the „Tarbor“ this was more of a fortified house than a castle. Evidence for the Tarbor comes in the form of a coat of arms which were granted to the town in 1476 and it is assumed that the structure dates from this time. Both the arms and the remains of the newer castle are however elusive and the nearest I can get to the original drawing is a copy drawn at the end of the nineteenth century.

Due to hundreds of years of confusion about which is the „Upper Castle“, which is the „Lower Castle“ and which is the fortified house, locating the ruins of the Tarbor involves two visits to Dürnstein. After drawing false conclusions on the lower terrace of the Medieval castle where Richard the Lionheart was imprisoned. Sifting through a plethora of irrelevant sites, a more through search on the the internet provides clarification. Returning to Dürnstein, I climb up to the old castle and leaving the main building on my right follow a path North. This leads out of the complex to a stairway formed by huge slabs of stone that winds its way intriguingly through the woods. Following this for fifteen minutes then brings me to what is obviously the Upper Castle. Perched on the brow of a hill, the Tarbor is surrounded by rocky crags from which the Medieval castle can be looked down upon.

Finishing the Dürnstein audio guide, I shift my attention to the Wachau News and Tips article, „Music in Krems, Stein and Dürnstein“. This I know is not as good as it could be and rewriting, I find myself conceiving of a CD of music from the region that reaches all the way from 38,000 BP to Beethoven’s last string quartet.

In Austria, the Christmas Season ends on 6th January, when according to tradition, the Three Kings leave Bethlehem to return to their respective kingdoms, with the Evangelists not saying whether these are geographical kingdoms or realms of knowledge. In the days immediately before their departure, children knock on doors and sing Christmas carols. Then a little hand holds out a basket and one makes a donation to a children’s charity. The donation made, an adult writes in chalk, above the doorway, the letters „C“, „M“, B“ and the date. The letters stand for Caspar, Melchoir and Balthasar, these being of course, the Three Wise Men who are about to depart.
2024, Week 3
Visiting a friend in Vienna, I am asked to explain the differences between the set of natural numbers, N and the set of real numbers, R. This is in connection with an article in a newspaper on a problem known as „Cantor’s Continuity Problem“. As this problem has consequences in the philosophy of mathematics, understanding this problem has been on my list of things to do for some time and the article prompts me into action. Although a chance prompting, what I write continues the December theme of getting to grips with the endlessness of the infinite and is written in a reader-friendly style with non-mathematicians in mind. Nevertheless, an introduction is called for:
Many decades ago, the idea was proposed that modern culture was rift apart by there being not one culture but two. Where the one culture was the sciences, the other was the arts and humanities. Now this feature is so embedded, both in our thinking and in our institutions, that the term „two cultures“ has lost its meaning and in daily life become a truism that nobody even notices. Although in contemporary art, under the banner of „Art & Science“, attempts are made at countering this, what results is so superficial and irrelevant that the attempts hardly even count. Contemporary culture is thus as inherently schizophrenic as ever. Largely atheist and purporting to believe in a scientific account of the world, the number of people who can give a coherent summaries of the Big Bang or of how life came to be and how we as a species evolved is deplorably limited. In the philosophy, instead of explaining things and providing us with a much needed foothold, the trend has been a drift away from the sciences and mathematics, towards the humanities and critical theory. Although the philosophy of mathematics might seem one of the more obscure and less relevant areas of human knowledge, the subject is of considerable importance not least as the modern world is based on mathematics. Yet the number of philosophers who are versed with the philosophical consequences of Cantor’s Continuity Problem, must today be assumed to be exceedingly limited. Filling the gap, there are mathematicians turned philosophers who confuse things by distorting the debate, for as mathematicians they think that when it comes to philosophy of mathematics, all that is involved is mathematics and the philosophy of mathematics. This is however not the case.
In philosophy of mathematics what is known as a Platonism position, is often seen as being out of date and tainted with the tart taste of the misplaced ideals that led to the rise of European fascism. Contrasting with this, is constructivism, which self-righteously presents itself as being impartial and it is this position that mathematicians turned philosophers invariably adopt. In doing so, they unknowingly pander to a view of evolution in which we see ourselves as lost babes in the wood, callously abandoned by nature in a world that cares but nought. For all its trendy, slick cynicism, this widely spread view is not only steeped in nineteenth romanticism but is also nauseatingly self-staged. Further, the implication is that as we cast into the world by chance, we are not really a part of it and thus have no responsibilities concerning it. In an age of climate change and defaunation this is both irresponsible and cowardly and allows a culture in which a comfortable form of defeatism is propagated and nurtured. This runs along the lines of all those who are no longer young saying, „Well by the time things get bad, I’ll be dead anyway“. Meanwhile those who are younger, are either genuinely afraid (as they should be) or must glibly place their hopes in technology and on green economic growth being somehow possible (see the Ulrike Herrmann on the Reloading Humanism People Page for a summary analysis of these hopefully out-sourced hopes).
As described in the essay „One World Pragmatism“ on the Mission Page, in an indisputably direct manner, pre-war philosophical debates on the nature of mathematics lead to Alan Turing and his team at Bletchley Park doing nothing less that knocking two years off the length of the World War Two. Today, changing our habits and the way we think, is essential to the establishment of a sustainable culture and as this means changing our attitudes to the world. Postulating numbers and mathematics as existent features of the world we live in is advantageous for the articulating of a philosophy in which a respect for nature is implicit. As expounded in the essay, One World Pragmatism, a Platonic position can also be used as a basis for explaining other problems which any useful philosophy must address, with physics and chaos theory both playing essential roles. Meanwhile, the article on Cantor’s Continuity Problem, given in Week 4 below, presents Cantor’s Continuity Problem in a reader-friendly manner and demonstrates that the problem and associated proofs are in accord with a Platonic philosophy of mathematics. With this, a last but well-hidden cornerstone is supplied, ensuring that One World Pragmatism rests on sure foundations. Soi e-a-o-u! Soi e-a-o-u!

In Stein, the life-affirming Humanese exclamation, „Soi e-a-o-u! Soi e-a-o-u!“, is given is given perfect expression through a concert given by a neighbour. The event is the last of a series of New Year concerts given by the Viennese Cabinet Orchestra in which my neighbour plays double base. The „orchestra“ is an ensemble of three, with violin and accordion joining the double base. The concert is in the „Salzstadl“ and beneath the impressively thick beams of a barn that was once used for storing salt, the ensemble plays to a full house. As the pieces played were written for orchestra, the arrangements are completely re-written. This is masterfully done and hearing the waltzes, polkas, songs and marches, one forgets that they were originally intended to be played by whole orchestras. For certain songs, singing along and providing rhythmic accompaniment through clapping are encouraged and the offer is enthusiastically taken up. The performance begins with Richard Strauss‘ Blue Danube, with which at midnight the New Year is traditionally greeted and which in the days that follow, begins every New Year concert. Iosef Ivanovici’s Donau Wellen is played and as in 1889, when it was first performed at the World Exhibition in Paris, is staggeringly impressive. For the New Year concerts the trio is joined by a soprano and there are arias and duos from Strauss‘ Fledermaus and from Emmerich Kálmán’s Duchess Mariza and Csárdás Princess. Classical songs such as Wiener Blut and Lieber Augustin are played along with the lively Tritsch Tratsch Polka. Augmenting this mix, there are the bitter-sweet tales of composers and song-writers fleeing Austria and beginning their careers all over again in the United States with Silvester Janiba’s vocals providing a perfect mix of Viennese charm, seen it all before pragmatism and humour. See: www.wienerkabinettorchester.at.
2024, Week 4
Over the course of the week, I slowly finish the article of Week 3. The result is an expanded introduction and answer to the article my friend asked me to explain. For the original article see: https://derstandard.at (Der Standard, 27.12.2023: Als Paul Cohen das Unendliche bändigte, by Reinhard Kleindl). For a reader friendly introduction to the subject along with my reply, click the toggle title below:

Two Takes on Cantor's Continuity Problem
Introduction
Where the real numbers are the numbers used in everyday mathematics, the set of natural numbers, N, is the set of numbers obtained by counting 1, 2, 3, et cetera, with zero added at the beginning. From N, the sets Z and Q can then be derived. Where the former contains all integers from minus infinity to plus infinity, Q is the set of rational numbers. These are the members of Z along with all the fractions that can be formed from Z. The next set is then the set of real numbers, R. In a simple world, R would be the set of all the numbers in Q combined with all the numbers that can be formed from the numbers of Q through quadratic equations. Quadratic equations are equations such as, x2 – 2 = 0. As the only solution to this equation is √2 the equation can be seen as being a part of the nature of √2. Equally, the equation, x2 – x – 1 = 0, can only be satisfied by 1.618… which is the irrational number phi. Although there are an infinite number of irrational numbers that can be defined by means of quadratic equations, there are other irrational numbers that cannot be defined in this way and which are fundamentally different. These are the so-called transcendental numbers which are also members of R. That a number could in some way be transcendental was first realised by the mathematician, philosopher, theologian, bishop and cardinal, Nicholas of Cues, otherwise known as Cusanus. For more on this, see the Laboratorium geometricum mellacensis accessible via the Reloading Humanism Mission Page. Although they cannot be defined like the other numbers in R are, transcendental numbers are members of R and as such are anomalous. Nevertheless, they are also exceeding important and some, such as pi, are well-known as a number can get. Completing the picture there is C, which is the set of complex numbers. Complex numbers are formed from real numbers combined with numbers from a new set, I. This set contains the so-called „imaginary numbers“. These are the roots of negative numbers which although they defy common sense, are in certain cases, useful and unavoidable.
During the nineteenth century Gregor Cantor saw that there was not just one form of infinity but that there could be any number of collections of infinite entities. This he proved by postulating the drawing up of a list which listed all the numbers formed from the fractions in Q between 0 and 1. This resulted in an infinite list from which Cantor then took the first digit from the first number, the second digit from the second number, the third digit from the third number et cetera, et cetera. Then he changed each digit by one. This resulted in the first digit of the diagonal number differing from first digit of the first number, the second digit of the diagonal number differing from the second digit of the second number and so on. By this means Cantor was able to demonstrate that the diagonal number was not on the list, with the method proving moreover, that not even an infinite list of all the numbers in Q could include the quadratic irrational’s and other numbers of R. This in turn meant there was a potentially infinite number of infinities. In geometry, Cantor’s diagonal method is equivalent to taking the diagonals of squares and rectangles. In the case of a square, if the sides are 1, then the diagonal is of length of √2 which as seen is a quadratic irrational. Importantly, the diagonal proof shows that the numbers in Q are not equivalent to the numbers associated with the set of points on any given segment of a line. Effectively, when one takes the sides of a rectangle with sides 1 and 2, one is counting out lengths using the numbers in Q. When one measures the diagonal however, one automatically jumps to another number system and assumes that any line between two points can be infinitely divided. This means that the algebraic irrational’s in R can be drawn upon and result in our being to say that the diagonal of the rectangle with sides 1 and 2 has a length of √3.
Prior to Cantor, it was known that the notion of infinity meant that as soon as a set of entities was defined, not only was there a potentially endless number of subsets but also of sub-subsets, with each subset containing yet another subset. In the case of N, there are, to name but two examples, the prime numbers (which can only be divided by themselves and one) and the complex numbers (which can be divided by numbers other than themselves and one). Both these subsets are infinite. Moreover the contents of both sets can be placed alongside those of N and matched up in a one to one manner. This makes them equivalent and even though we think of the set of prime numbers as having less members that the full list of natural numbers, in fact this is not the case. This is because both are infinite. All this can be summarised by saying that there are more infinities in the subsets of N than in N itself. Far from being paradoxical, this is integral to the nature of infinite collections. Where N is a plain case of counting out, one two, three, …, the subsets of primes, complex numbers, odd numbers, even numbers, numbers that include the digit 3, numbers that do not include the digit 3, numbers with sequences such as 2,3 or 2,3,4, embedded either once or repeatedly somewhere within them, et cetera, et cetera (ad infinitum), imply a different degree of infinity. The degree of difference of infinity between the infinity of a set and its subsets is called by mathematicians, the cardinality of the set. Starting with any given set, such as that of natural numbers N, a set is said to have a degree of infinity N–0 (properly written by mathematicians as aleph subscript nought). The subsets of N are then said to have a degree of infinity of 2(N-0), the degree of infinity of the sub-subsets of N is 2(2(N-0), et cetera. Meanwhile the cardinality of the segment of a line is represented by c (properly written as a lower case gothic script, c). Importantly it can be proven that the cardinality of the subsets of N is equivalent to the cardinality of the line, so that:
2(N-0) = c.
Although mathematicians introduce the notion of cardinality by beginning with the aleph nought associated with N, with reference to the cardinality of the line one could also start with Q. In other words, the difference in cardinality of the first set taken and the cardinality of the line is always of the order 2(N-0). Both the line and the number of subsets in a set are infinitely infinite when compared to the contents of the initial set which is merely infinite. Cantor’s Continuity Problem is thus the question of whether there are other forms of infinity apart from N-0, 2(N-0), 2(2(N-0)), 2(2(2(N-0))), et cetera. Can there be an infinite set that has a degree of infinity, that is between these degrees of infinity? With respect to the segment of a line and continuity, the question is of whether there is a set of points that are infinite but which are not equivalent to the whole segment? Accordingly the problem is also known as the continuum hypothesis as the existence of such a set would upset the continuity of the continuum of numbers arranged along the line. Cantor assumed that the answer to these questions was „no“ but could not prove it. As the existence of such a set undermines the central assumptions of set theory and infinite collections, a positive answer can be seen as amounting to a contradiction in set theory. Independently, Gottlob Frege in Germany and Russell and Whitehead in Britain, were using mathematical logic to construct foundations for mathematics that rested on a bedrock of logic to which set theory was integral. For this reason, in 1900, David Hilbert put Cantor’s Continuity Problem at the top of his list of problems in mathematics that needed solving. In philosophy of mathematics, Hilbert was a formalist who believed that mathematics was a closed, purely formal system which was governed by rules that enabled everything to be proved. This meant that all truths were deducible, with no falsehoods being derivable. Moreover, while falsehoods could not to be proven true, they could be proven to be false, so that their falsehood was thought of as being an integral part of the system. In 1936, this cut and dried view of mathematics was dis-proven by the Czech mathematician and logician, Kurt Gödel. In his celebrated Incompleteness Theorem of 1936, Gödel showed that, as a system of deducted truths, mathematics could never prove all truths and could not prove that falsehood was excluded. Though there remained the possibility that provable statements might somehow be distinguishable from unprovable ones, this was disproved by Alonzo Church in 1936 and then by Alan Turing in 1938. In the light of these results, Quine, in a pruned and more efficient version of Russell and Whitehead’s Principea Mathematica, included Gödel‘ Incompleteness Theorem as an integral and unavoidable part of the system. In 1947, Gödel went on to show that the continuity of the number series assumed by Cantor, could not be disproved. Far from leaving mathematics in disarray, Gödel’s Incompleteness Theorem accords perfectly with a Platonist philosophy of mathematics in which mathematics and the entities postulated by mathematicians are seen as existing as objective features of a material world in which matter/energy is arranged in space. This makes mathematics a process of discovery that is analogous to science and Gödel himself subscribed to a Platonist view of mathematics. From such a standpoint, the fact that not everything that can be discovered should be provable within a formalised system is hardly surprising. Putting the Platonist position in modern terms, where mathematics deals with the relations between sets and sets of sets that derive from the relations pertaining between things in the outside world, science deals with relations that derive directly between things in the outside world. This makes mathematics an abstract copy of the world and its processes. Mathematics is therefore of use in describing the physical world for the simple reason that the physical world is mathematical.
In 1963, the American mathematician, Paul Cohen, developed a new method of proof known as „forcing“ and used it to show that collections of entities could be generated, that disrupted continuity. This means that whilst continuity cannot be proved false, equally, it cannot proved be true. The word „forcing“ suggests the use of brute force-like techniques, yet Cohen’s techniques are sophisticated and subtle and involve a set that is not constructed in the usual way but rather is indirectly invoked so that when an infinite number of such sets with a cardinality of 2(2(N-0)) are placed inside a conventional set, the new sets of sets are invisible and cannot be counted. This means that the overall containing set has a cardinality of 2(N-0) as opposed to the 2(2(N-0)) which it ought to have. As on this model, the line sequence, c, is defined as having a cardinality of 2(2(N-0)), this means that between N-0 and 2(2(N-0)), there is a set of cardinality 2(N-0) which goes against the hypothesis of N-0 and 2(2(N-0)) forming a smooth and continuous continuum. While this does not disprove the continuum hypothesis, by throwing a spanner in the works, it shows that there cannot be a proof that will prove it to be true. In the print edition of The Standard, Kleindl’s article is concluded with the words „The infinite escapes analysis“. In the on-line edition however, his conclusion is longer and he says:
There thus remains the recognition that there is no denying that certain properties of the entities dealt with by mathematics are chosen. The continuity hypothesis can be assumed to be either true or false without either decision causing problems for mathematics. The nature of the infinite is not a metaphysical reality that can be approached through the use of logic. It must be assumed as a credo of belief. Mathematics does not spare human beings from deciding how they imagine the infinite to be.
Although the most simple and reasonable explanation as to why mathematics works, in today’s cultural climate, the Platonic idea of mathematical entities being existent features of our universe and of the multiverse that contains it, is unfashionable and replacing formalism, a new position was been formulated. This is constructivism and this is clearly the view of mathematics to which Kleindl subscribes. In constructivism, the human perspective and the process of mathematicians doing mathematics is emphasised and a direct, one to one connection to the physical world is denied. In constructivism mathematics is seen as being akin to an arbitrarily constructed system of scaffolding. This relates to the physical world by virtue of the fact that so many additions and extensions have been added on, that somewhere, somehow, something is always useful in describing a processes in the physical world. Nevertheless, ultimately mathematics is a purely human invention that in reality has nothing to do with the physical world. Put in terms of aliens arriving from outer space, on a Platonic view, even if we and the aliens had nothing else to talk about, we could talk to them about mathematics, just we could talk to them about atoms and other physical entities. Following constructivism however, this would not be possible as the aliens would not be able to follow our purely subjective ways of thinking and vice versa. For the constructivist, Cohen’s consumate and highly influential proof provides a perfect example of the improvised, pasted together nature of mathematics.
Take One
As a way of getting to grips with what Cantor’s Continuity Problem is about, I develop a model in which I endeavour to visualise the basic number theory of N, Z, Q, R and C. The result is then a model that whilst it does not say anything new, through the step by step way it which it is explained, makes clear the nature and place of transcendental numbers. On a straight line, a unit length is defined and from a given point, lengths are marked and counted out towards the right. On the diagram, this process brings into being the set of natural numbers, N. Then the same is done in the other direction. This defines the x-axis and brings Z into being. Next, a 3,4,5 triangle is constructed with the 90° angle that is integral to the triangle being placed at zero. This is unproblematic as at this stage, the only points which can be identified and thus are available, are those designated by coordinates those with whole numbers. The 3,4,5 results in a perpendicular which when extended so as to cross the x-axis, can be marked out in the same way so as to create a y-axis. In order to generate Q, the x-y co-ordinates of all of the points thus far defined are taken and each whole number on the x-axis is divided by the whole number on y-axis. As on Cantor’s list, where x is smaller than y, this results in the rational numbers formable from fractions that run from zero through to one. Where x is larger than one, the result is then all the rational numbers formable from fractions that run from one to infinity. Both these sets are infinite and equivalent even though the length associated with zero to one is a finite length and that associated with one to infinity is unending. As the same is true for any other set, such as the set of numbers between two and three as compared with the set of numbers from 3 to infinity, continuity is implicit and was assumed by Gödel in his 1947 proof that continuity could not be disproved. If the numbers thus generated are marked off on the x and y-axses then Q and the notion of continuity will been embedded into the model. In the next step, with zero as a starting point, each pair of points identified above is seen as defining the points of a triangle and using Phytagoras‘ Theorem, the length of the hypotenuse is derived. This results in the generation of a whole host of numbers, some of which are new. Among the new numbers there will be √3 which derives from the triangles formed by the points, (0,0), (0,2), (1,2). The first pair of points, (0,0), (1,1), is a infinitely thin triangle with a hypotenuse of √2. Triangles with infinitely thin bases and which so amounted to lines were first postulated by Cusanus. The host of new numbers generated in this way are the quadratic, or algebraic irrational’s. As was the case with Q, these numbers can be marked off as lengths on the diagram and integrated into the model.
The point of the model outlined above is that although three infinite collections of numbers have been generated and marked out, transcendental numbers have not been arrived at and moreover cannot be arrived at as the rules used are not capable of engendering them. Although using Phythagoras‘ Theorem, a circle may be defined as all the points that satisfy the equation, x2 + y2 = r2 and although this can be expressed in quadratic terms as, (x2 + y2) – r2 = 0, nevertheless all that may be ascertained about any circle drawn, is the data that can be derived from the co-ordinates of the points contained within it and on its circumference. These range from the obvious fact that the diameter is twice the radius, to more interesting facts concerning the properties of the regular and irregular figures with corners that lie on the circumference. However, of the length of the circle’s circumference and of its area, nothing can be said. Rather, these features, which nevertheless clearly exist, can only be empirically ascertained by rule of thumb. This leads to the realisation that there is a hitherto unidentified number involved. This is the number pi and slowly it becomes known that whilst pi can be approximated to, like the other irrational’s, its enumeration is unending. Even so, this new number differs from the other irrational’s due to its being indefinable in terms straight lines and quadratic equations. This fact was first appreciated by Cusanus who saw that any attempt at squaring a circle was inevitably circular. As the area of a circle is pi multiplied by the the square of its radius, in order to square a circle of radius r, one must either construct a rectangle that is πr x r, or a square that is √πr x √πr. This however invokes precisely that which is not known and which is not only not on the model outlined above but moreover never can be.
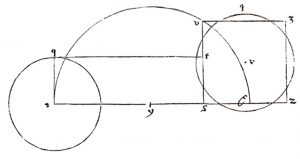
In the above diagram, the circle on the left-hand side has a radius of length 1 and the rectangle formed from it has of length π, so that the area of the rectangle is the area of the circle. If the side of the rectangle of length π is extended by 1 and the resulting length is divided in half, using this new division as centre, the large semi-circle shown above may be constructed. This has a length that is equal to the circumference of the original circle. The right-hand side of the rectangle is then extended up as far as the semi-circle. Using this new length, a square can be constructed that, with sides of √π, squares the original circle. Cusanus saw that pi was transcendental and different from the other irrational’s. Transcendental numbers are difficult to identify and once found it is difficult to prove that they are transcendental. Accordingly Cusanus was not aware that there were other transcendental numbers apart from π. So far, modern mathematics has identified some sixty numbers and classes of numbers that either are, or may be, transcendental. It is possible that there are an infinite number of transcendental numbers but this is not known. Like Cantor’s Continuity Problem, the existence of transcendental numbers that defy iteration and defy formulation through the use of quadratic equations, appears to demonstrate the constructed, artificial nature of mathematics as a human and thus subjective activity. Nevertheless appearances can be deceptive.
On the model, the construction of the 3,4,5 triangle elementary as on the diagram as it existed at that stage, the concept of an infinitely divisible line had no been introduced and the only numbers that were available were the whole numbers of Z. It was only once the numbers of Q had been defined that the infinitely divisible was brought into being. Thus now, in order to now construct a 3,4,5 triangle, one of two techniques must be either used or invoked. The first is the method of proceeding by trial and error. In the case of a 3,4,5 triangle constructed through trial and error, the point required is approached through „judicious judgement“. This draws on what is known as „the axiom of choice“. This is the assumption that from an infinite collection, a choice can be made and is necessary as not only the area identified as being likely to contain the point in question but also the dot that later marks it, both consist of an infinite number of extensionless points. Thus the axiom of choice must be invoked in order for a decision to be made. In the above, the axiom of choice tacitly invoked with the introduction of the notion of an infinitely dividable line and in his proof that continuity could not be proved false, Gödel used the axiom. Alternatively, instead of invoking the axiom of choice, the principle of rotation may be introduced. This means that a circle can be constructed using a ruler and compass. Drawing arcs, a 3,4,5 triangle may be constructed by drawing arcs of lengths four and five from the two ends of the line of length three. Despite appearances, the two methods of constructing a 3,4,5 triangle are related. This is because if a point is imagined from which an infinitely long straight line extends outwards, then if the line is rotated in a single direction about the point, it will sweep through all the other points on the plane concerned. If however the point is abandoned and the infinitely long straight line is moved through the plane in a single direction following a path that is straight and which lies at angle to the line, then the infinite extent ahead of the line will be swept through. However behind the line’s original position, there will be points which will have been ignored and no matter how far back the starting position of the line is shifted, there will always be points behind it, which cannot be swept through. The relevance of this to the axiom of choice, is that the infinite line rotating about a point, sweeps, scans and encounters all the points on the plane in which the point is embedded. Having encountered them, it can then, theoretically at least, make a choice about which point is to be selected for a given purpose. A point associated with a straight line that moves ahead in a single direction cannot do this. On the model, this means that as soon as the notion of an infinitely dividable line has been introduced one is justified in drawing circles and one is justified in trying to elucidate the nature of π as well as other non-quadratically definable numbers that circles and the functions of circles suggest might exist. Nevertheless their elusiveness means that they will never find an exact place on the x and y-axses that is equivalent to and equitable with the way that quadratically defined irrational’s can be slotted into their appropriate places on the axses. As argued, the axiom of choice invoked by Gödel is a sweeping and circular, all-embracing notion that reaching out, not only allows choice but inadvertently and inevitably, enables transcendent numbers to sneak into the picture. Not introduced by proper definitions, they are in effect surreptitiously ushered in through the back door by something that is there and yet which at the same time, lies outwith the system. Gödel’s adoption of the axiom of choice contrasts with the proof developed by Cohen in which the axiom of choice is denied. Where one can characterise Gödel’s proof as involving top-down decisions, Cohen’s approach is bottom up. Where Cohen proceeds from inside sets, whereas Gödel starts from outside. For constructivists, the conclusion to be drawn from the two proofs is that it is up to us to decide whether we want there to be continuity or not, this underlying the constructed nature of mathematics and its ad hoc relation to the world of physical things. Yet this is not necessarily the case and the Platonist can argue that when we do mathematics, we continually jump between a conception in which the line is divided according to the numbers derivable from Q and the quadratic irrational’s of R and a different conception that involves the transcendental numbers. These latter are seen as acting as strange attractors which can be approached through iteration but which but never fully elucidated or expounded. Unlike the constructivist view of mathematics, this is seen as something that in reality corresponds to the very real differences between linear and angular motion. Although the transcendental numbers transcend the bounds of the straight line number systems, they are not a subjective phenomenon or projections but rather are an integral, immaterial facet of reality. Cohen’s proof suggests that between the ordered chains of subsets and sub-subsets that the other numbers of R bring into being, the set and sub-sets of transcendental numbers do pop up as sets with a potentially in-between, ambiguous status. Within the world of straight line geometry where parallels lines never meet and where there are no transcendental numbers, the rock solid foundations that Hilbert envisaged are as solid as ever. Yet as soon as rotation is introduced, a new geometry of curves and arcs becomes woven in with the geometry of straight lines and in number theory sets pop up which, following Cohen, confound the order of the straight line way of seeing things. This gives an appearance of disarray but may well instead be a new form of order. This however depends on the nature of transcendental numbers, whether they are infinite in number and whether their cardinality is equatable with that of other sets. Should the cardinality of the set of transcendent numbers be equatable with that of the natural numbers or any other uninterrupted infinite set, then sets of them are not disruptive in the way demonstrated by Cohen. Transcendent numbers can then be imagined as joining the other numbers in R on the same line. Alternatively should they be disruptive, they can be treated like the imaginary numbers. Imaginary numbers are envisaged by mathematicians as being arranged along a y-axis, so that with the numbers from R arranged along the x-axis, all possible combinations of the two may be arrived at, thus forming the set of complex numbers, C. In the case of transcendent numbers, the same may be done with all the numbers of set Q arranged along the x-axis together with all the irrational numbers expressible by quadratic equations. With the transcendent numbers arranged along the y-axis, the result of all possible combinations then gives R. Either way, the important point is that the work of Cohen and Gödel can be interpreted in a Platonic manner and does not necessarily imply a constructivist philosophy of mathematics.
Ramifications
In mathematics and applied physics, it is a well-known fact that moving entities that have the capacity to mutually affect their movement, will synchronise or phase-lock. This takes place following ratios that are determined by rational numbers. Over time, ratios that involve irrational’s are rejected and more stable rational combinations win out. In the case of Jupiter and its neighbour Saturn, the time of orbit of Jupiter around the sun, relative to that of Saturn, is exactly 2:5, this being reflected in a coupling of their phases of eccentricity. The same phenomenon can also be seen when the eccentricities of the Uranus are compared with those of its neighbour Neptune, or when the eccentricities of Venus are compared with those of Earth. The rotations of planets about themselves can also become locked-in with another source of periodic or semi-periodic motion. In the case of Mercury, the planet’s spin about its axis has become locked in with its orbital frequency. This is fixed at a ratio of 3:2 so that a day on Mercury lasts two Mercury years. So well-known that we take it for granted is the moon, whose rotation about itself is phase-locked in a 1:1 manner with its rotation around the Earth. It is for this reason that we never see the moon’s other side. For the mathematician Manfred Schroeder (Fractals, Chaos, Power Laws, Notes from an infinite Paradise, p. 242):
Thus we have to face the curious fact that the tinniest distinctions — the differences between rational and irrational numbers and, among the irrational numbers, between normal and non-normal numbers — make a decisive difference in the final fate of a numerical iteration. Ordinarily, one should think that physics, and certainly the tangible world at large, would be untouched by the purely mathematical dichotomies between rational and irrational numbers or normal and non-normal numbers. But in reality this is just not so. While, true enough, though everything in the real world can be adequately described by rational numbers, it so happens that a mathematical model that distinguishes between different kinds of numbers is not only useful but catches the true, possibly hidden, spirit of the problem.
The question, „Why does phase-locking take place?“ suggests that as implied by the model expounded above, the members of the two sub-sets of R are genuinely more complex than the members of Q, with this being something that exists out there in physical reality so that physical processes in reality respond to this distinction. This however implies and necessitates an unequivocal endorsement of a Platonic view of mathematics and its relation the physical world. The more detailed explanation of the answer to the question of why phase-locking takes place, is because in dynamic processes, over time, simplicity is evidently more sustainable that complexity. The underlying ultimate justification of this is that, although there are various kinds of space and although the Theory of Relativity means that space can be warped by immensely dense things and by things travelling at speeds approaching that of light, nevertheless physics has shown that by and large, our universe consists of un-distorted, Euclidean space. This in turn means that following a Platonic view of the world, the straight-line geometry that is a feature of the number theory model introduced above, is an accurate summarisation of the way that relations pertaining between things in the physical world may be abstracted and formed to make sets and sets of sets et cetera, with the differences in complexity pertaining between sets at different positions on a nested chain of sets being real and thus, on occasion, playing a role in how dynamic, non-linear physical processes evolve. Summarising in simple terms, in dynamic systems, ratios involving „diagonal numbers“ such as √3, being more complex, are less sustainable than ratios which consist solely of whole numbers and this is an objective facet of the way things are in our universe and is not a projection. Here it is important to emphasise that the fact that our universe consists of Euclidean space, is an empirical fact, with non-Euclidean geometry only coming into play in the vicinity of stars and of black holes. As proof that this an empirically derived conclusion and not a projection, is the fact that physicists were expecting the results of the above observations and calculations to show that we live in a curved, hyperbolic space. That this is not the case is due to the existence of a mass, dark matter and an energy, dark energy of which currently nothing is known except that they are there and that it is dark energy that straightens out the hyperbolic space that physicists were expecting. From this recognition, physicists conclude that where the sum total of what physics knows about the world account for 5% of the mass/energy in the universe, dark matter accounts for 20%, with dark energy accounting for the remaining 75%. The above explanation of phase-locking, is thus won at the price of accepting that 75% of mass/energy in the universe is unaccounted for. Nevertheless its simplicity is undeniable and to deny that this explanation has a foundation in the physical world, the constructivist must resort to convoluted and unconvincing explanations as to why the above is nothing all but a series of projections and assumptions. The constructivist account of mathematics thus challenged, one can move on to re-evaluating the results of Gödel and Cohen’s work in the wake of more recent developments in the fields of physics and mathematics.
As a universe expands and runs its course before dissipating back into the multiverse from which it came, it goes from a state of minimum entropy to a state of maximum entropy. This does not take place in a even manner but rather in a manner that is erratic and unpredictable. Along the way, from out of randomness and disorder, islands of order repeatedly emerge. Chaos theory describes the coming into being and fading of order as the universe pursues its course towards maximum entropy. Taking a cue from chaos theory, instead of seeing the results arrived at by Gödel and Cohen as indicating that it is a question of belief whether one assumes the continuity hypothesis or not, one can see it as indirectly acknowledging the fractal, non-linear nature of the universe. This means that we as individuals do not have to decide, once and for all as a matter of credo, whether we adopt the continuum hypothesis or not. Rather it means that whether we assume it or not is a matter of context, use and occasion. Far from implying some sort of spurious form of subjectivity, such an interpretation accepts the fundamentally fractal nature of the physical world and the inherently indeterminate nature of non-linear, dynamic systems. In the physical worlds of both living and non-living things, it is non-linear processes that predominate and not linear processes. Thus even in a supposedly simple case where two bodies which are capable of mutually interacting are combined with a third, which latter, whilst affecting the movements of the other two is not itself affected by them; if a powerful injection of energy is injected into the system, the movements of the two inter-related bodies is, even in this simple case, unpredictable. In planetary physics, the upshot of this is that despite its apparent stability, our own solar system with its eight planets and one down-graded ex-planet, is no longer seen as a paradigm of order and stability but rather is classified as being „semi-chaotic“. The indeterminacy and relativity that Gödel and Cohen’s results imply can thus be seen as reflecting not only the nature of mathematics as it is conducted by human beings but also the fractal and non-linear nature of the world that is out there and which we all too often ignore or are ignorant of. Thus contrary to what Kleindl says at the end of the on-line version of his article, the nature of the infinite can be seen as a metaphysical reality that is approachable through the use of logic (and mathematics). The wacky nature of this new form of Platonism was anticipated by Cusanus in his De doctra ignoranti, in which not only did he see an infinitely high triangle with a finite base as a straight line but also saw a straight line as the segment of a circle of infinite radius. Here of course, things dissolve and boundaries blur but that is perhaps inevitable when straight line geometry and circular geometry are combined.
Take Two
After completing his paper, Cöhen asked Gödel to look over it, so as to verify the steps of his argument and his approach. This Gödel did, endorsing Cohen’s work. Later the two met and although they talked about continuity, Cohen had the impression that Gödel was being cagey. This he suspected, was because Gödel was hiding the fact that he saw the problem and the delivery of some form of positive answer as being essential to the maintaining of a Platonic view of mathematics and yet, was unable to make any headway in working towards the for him, much desired answer. Despite his genius, like everyone, Gödel was a child of his time and it is likely that he saw mathematics as a fixed structure of crystalline clarity, that was not subject to change and was not in any way amorphous or ambivalent. Today, the way we see the world has changed and modern physics sees our universe as being embedded in a multiverse of elementary particles. Continually expanding, the multiverse is like a pot of boiling water, with each bubble of steam being a universe that after exploding, expands until it is eventually absorbed back into the multiverse from whence it came. This is possible as the multiverse expands faster than the exploding universes it contains. Meanwhile, the answer to the question, „What lies beyond the multiverse?“ is simply, „More multiverse.“ In the multiverse, although endless reaches of approximately even distribution predominate, there are also patches of dense distribution and patches where elementary particles are scarce. The endlessly endless nature of the multiverse and the endlessness of the eternity that is at hand, mean that within the dense patches, patches arise which are ordered and structured in ways that result in crystalline structures of immense heat and immense density. These are capable of acquiring degrees of order that exhibit what physicist call „super-symmetry“ The super-symmetry is however unstable and soon enough, a tiny flaw emerges. Upset by the flaw, the construction shatters and an exploding universe is engendered. The forms of scattering that lie behind the genuinely random distribution of the multiverse range from the almost empty, to sparse, average, dense, super-dense and ultra-dense, with each form having the capacity to give rise and fade over into one of the other forms. Moreover the patterns of distribution are self-similar. This means that if zoomed in on, the same basic patterns will be encountered. As our universe emerged from out of the multiverse, the principle of random but nevertheless self-similar distribution is continued and is a feature of the way that clusters of galaxies are distributed. Zooming in on these clusters, the pattern is repeated by the ways in which the galaxies contained by the clusters are arranged. Inside galaxies, the pattern is continued by the clusters of stars and then again within the clusters, by the distribution of the stars themselves. Taking a Platonic view of mathematics and seeing it as an abstracted reflection of physical reality means that it is hardly surprising if, in our number systems, within infinite collections, non-equivalent collections should have the capacity to suddenly pop up when forcing techniques are applied. For this can be seen as reflecting the fact that within the infinitely infinite reaches of the multiverse, there are always universes coming into being and which contain within themselves, collections that over time are subject to changing degrees of infinity. This suggests that the real problem is not continuity or the lack thereof but rather the way in which we see infinite collections in number theory and their embedding contexts. Taking a Platonic stance it may well be that the weird, wacky way in which non-equivalent collections can pop up when forcing techniques are applied, simply reflects the weird, wacky nature of physical reality itself. When asked to draw a randomly distributed set of dots, people will invariably draw random distributions that whilst random, are not genuinely random and do not feature the forms of scattering listed above. This shows how we are adapted to and used to a world of linear continuity. With respect to set theory, this in turn means that we expect infinite collections to behave in the same way as finite collections and yet as already encountered, they do not. The upshot of this is that in order to shore up set theory, one should say that as soon as one moves from the linear world of finite collections and collections that only extend as far as Aleph Nought, over into worlds where there are collections with higher degrees of infinity, different immediately considerations apply. Although making this move shakes the foundations of set theory, this can be seen as being akin to way that space is bent by black holes and when space craft travel at speeds approaching that of the speed of light. Although in the vicinity of a black hole, space is bent and Euclidean geometry no longer holds sway, this does not mean that it is disproved, only that a realm has been encountered where it is no longer valid. What is disproved is the assumption that Euclidean space is the only kind of space that can exist but that was already disproved during the nineteenth century by mathematicians who demonstrated that although counter intuitive, non-Euclidean spaces were consistent and feasible. These physics-based considerations, combined with a Platonic view of mathematics, thus provide an alternative context for taking a relaxed view of continuity that is not necessarily related to questions concerning the ultimate nature of the transcendental numbers.
2024, 25th January

Confirming the first of the alignments arrived at in Week 47 of 2023, I find that on the 25th January, if on the Goldberg above Stein, one looks from the statue of Jesus hanging on the cross towards the West, this is indeed the last day when the sun sets over the hills in the middle distance. Under suitable atmospheric conditions, this results in „red sky at night, shepherd’s delight“ sunsets. After this date, as the sun climbs higher in the sky and moves North, instead of setting, it simply disappears behind the wooded slopes of the hills in the foreground. The first of these hills is the Pfaffenberg where there is a path that leads towards the point where on this day the sun auspiciously sets. From this time on, from the Schreckberg Cross, no more dramatic sunsets will be seen. The transition is a sign that although the winter is far from over, the days are getting longer. This is the first of a series of solar events that make the skyline a form of calendar which over the course of the year will be documented photographically. The 25th January is significant as it is the day when the poet Robert Burns was born and in Scotland the day is celebrated with a meal and recitations of Burns‘ poetry. In Scotland, Burns Night can be seen as a secular substitute for the Christian festival Candlemass, which is not celebrated by the Scottish Church. Thus at Reloading Humanism, the 25th January is the beginning of a period that extends up until 7th February, when the end of winter is celebrated through a celebration of Robert Burns and the eating of haggis. For the reasoning behind this see the 2023 entries of Week 47 followed by the 2024 insights of Week 5 below. For an image of the sun rising over Weather Cross Chapel and a guide on how to make a haggis from raw ingredients wait for Week 6!

Below the Goldberg on which the Steinerkreuz stands, there is the Kesselhaus Kino or „Old Boilerhouse Cinema“. With a celebration of Burns and his poetry postponed, this is where I am on the evening of 25th January. Here Anna Schmidt’s Living Bach is screened. Although as a documentary, the work is flawed through the inclusion of too many people and a lack of focus, the film is nevertheless inspiring. It also answers the questions of why Bach is special and why today, his music is played, sung and loved by people the world over. As my introduction to Bach is through Douglas Hoffstadter’s 1979 book, Gödel, Escher, Bach, an Eternal Golden Braid, when I listen to music, the more obviously mathematical works of Bach, such as A Musical Offering, The Art of Fugue and the Goldberg Variations, rounded out with The Brandenburg Concertos, are among what I listen to. Thus the film was an important reminder that many of Bach’s are so staggeringly beautiful that it makes people cry for joy. In my case, the work that hits me is the Air on G String from Orchestral Suite Number 3, this being the music with which the soundtrack of the film begins.

In the film, people form all over the world explain why they find Bach’s music uplifting and how it opens them to an awareness of there being something higher. This process however is not so much an abstraction away from life but rather comes out of life and repeatedly the people interviewed, although they come from cultures as far removed from Baroque Europe as one can imagine, say how Bach knows and articulates sadness, grief, bewilderment, frustration and confusion, and yet in all this there is for them, always a message of hope written into the music. Coupled with this, is the way in which the different voices in Bach’s music are interwoven in a continual dialogue with each other. In the world there are over 300 amateur choirs all dedicated to singing Bach’s choral works. Repeatedly it is said how singing in such choirs is uplifting and how through the dialogues between the different voices, a sense of togetherness arises, as each singer knows that they are playing a part in creating a majestic whole of staggering beauty and grandeur. Bach’s music is thus deeply humanist and in the film this point is made by an IT worker from South Africa who says that had Bach ruled the world, racism would never have found a place. He also says that after the segregation of apartheid, it was Bach who made him believe that people from different ethnic backgrounds can live together.
As I was expecting, the film prompts something and walking home, I realise that for me, its purpose is to provide an opportunity for expanding the formulation of Neo-Platonism given in the One World Pragmatism essay. This mathematical sketch I see, is begging to be rounded out and expressed in terms of music. Following chaos theory, the stability of the natural world rests on the stability of the populations of the millions and millions of different kinds of living things. If we are to survive, we must learn that any small upset in this delicate web of interrelated balances will always have the capacity to undermine the stability of the system as a whole, potentially wreaking havoc in the world of human affairs as elsewhere. Like the populations of living things, music and the stability of musical tones and their overtones can also be explained in terms of chaos theory. One can thus follow Plato in his Timaeus and say that the world as we know it is the result of the harmonies that one can be described as being musical or akin to music. Around the Equator, these harmonies are unchanging, whilst beyond the Tropics, in the Northern and Southern Hemispheres, were the stability of living things to be translated into music, the tones would be continually changing in accordance with to the cycle of the seasons. This is because with the seasons, populations rise and fall, as insects proliferate and then die, prompting the birds and mammals that feed on them to either migrate, hibernate or to suspend procreation. Climate change is affecting this music and creating dissonance. If nothing is done, chaos will result, rapidly followed by changing phases of stability in which the new mixes of living things may not be to our advantage. In one worst case scenario, populations of pests may suddenly explode, destroying harvests over whole continents. Insects that bite will in any case spread and with them our susceptibility to the diseases they bear. Whilst millions of specialised forms of life will vanish, sea gulls, carrion, rats and other scavengers will flourish. Whether we will be able to adapt to what may well be sudden changes, is an open question and for this reason, Einstein saw the fate of humanity as being linked with that of bees. No bees, no humans. Put in terms of music, the intricate mix of tones with ever-changing harmonies and counterpoints, will turn to a monotone dirge that is likely to announce the end of culture that caused it and quite possibly the end of ourselves as a species. In the film, an interviewee from Australia describes how she nearly died and lost her house in a forest fire that for miles around, blackened the landscape. Three days after the fire, she went out into the forest and among the burnt trees where birds no longer sung, she played Bach on her violin. The music of Bach gives hope that, through the appreciation of the harmony generated by the interaction of many voices, understanding for the subtle complexity of life and the world we live in, may grow and become a mainstream tenet of what we believe. Given the way contemporary culture is going however, this is a very slim hope indeed but it is there and as Bach shows, has the capacity to be staggeringly beautiful.
2024, Week 5
Prompted by the King’s Theme of A Musical Offering, I see that the solar alignments associated with the cross on the Goldberg could be turned into notes. This would involve constructing a circle with the notes of the octave arranged around it and an inner inner wheel on which the alignments are shown. The plan would then be to give it to Martin and ask him if, in whatever key he wishes, an interesting melody might be concocted from the notes that the alignments pick out. But then doubt strikes and I suddenly see the alignments on which everything depends, as being too slight to be of any real significance and the whole endeavor as something can be dismissed with a simple, „So what?“ or „And?“ This would make the weeks of work since November nothing but a waste of time. Nevertheless, used to the up’s and down’s of creative work, I return to the drawing board and re-examine the alignments of 25th January and 3rd February (confer Week 4 above and Week 47 of 2023). To my surprise I see that if extended northwards, the lines on the map follow the lines observations made the year before and point to the places on the skyline where, from another project, I know that the sun rises and sets on the day of the summer solstices. This is a result of my moving the central point out of the vineyards to the point marked by the cross. In one direction the shift makes no difference, in the other it works to my advantage. Underlying this, is the parallax caused by the hills which also works in my favour. Not something that I had even dared hope for, the alignments are nevertheless real and are there! The dates between which the Burns Night is held are thus determined by the inversion of the bearings of the rising and setting sun on the day of the summer solstice. This changes everything and makes the 13,14,15 triangle enclosed in a circle a convincing and satisfying image of the year. Moreover the reference to the statue of Saint Vitus in a Vat is confirmed, as if the line that points North is extended South, it passes through Schloß Baumgarten, where in 1943, the sculpture was consigned for safe-keeping for a number of months before being stored in a mine at Altaussee (for more on this, see the article The Triangle and the Saint from Krems). Measured from the bottom of the perpendicular, the apex of a 13,14,15 triangle is shifted away from that of a equilateral triangle by 14.5°. Taking 15° as an approximation for this means that if the outer circle is divided into 24 segments, the 13,14,15 triangle can be approximated to. Likewise, the rising and setting of the sun on the days of the winter solstice can be approximated to if a deviation of 2° is accepted. Meanwhile the equally tempered octave is introduced by taking every second 15° division as representing a half tone. Constructing wheels, I then add a drawing as a background. As it is not up to me to define the key or the system of tuning, I leave the divisions on the outer wheel blank and fix the inner wheel to the background so that the musical divisions can be rotated.
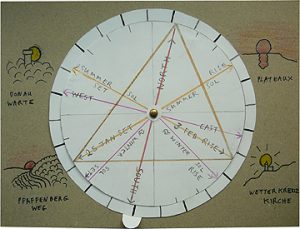
After nine and a half years living in Stein, I have at last found a way of relating to and communing with the landscape in which I live and where I take my constitutional walks. Nevertheless theory has yet to reveal itself in practice and for this I must wait a few more days.
3rd February, 2024
After a brisk walk up to the cross on the Schreckberg, I wait for the sunrise and am relieved to see a dark band of cloud being blown northwards away from Weather Cross Chapel and the predicted place of the sunrise.

Happily, everything works out as predicted, from out of the dip below the church, the sun slowly begins to rise.

As it it climbs and edges its way South, by the time it is half-risen, it is exactly over Weather Cross Church, which due to the absence of obstructing cloud, is dissolved in a blast of blazing light that heralds the beginning of a new day.

Returning home, on the console table in the hallway, I substitute the object that represents Yule with the object that represents Imbolc. Soi e-a-o-u! Soi e-a-o-u!

Although earmarked as a possible date for the holding of a Burns Night and despite the week’s astronomical breakthrough, fate has long decided that 3rd February 2024 should be marked by something other than a haggis being cut open to the accompaniment of bagpipes. Thus instead of spending the day in the kitchen, the afternoon finds me on a regional train chugging through the Lower Austrian countryside.
As I slowly make my way towards Saint Pölten, the regional capital of Lower Austria, I read an interview with Johannes Vogel, director of the Natural History Museum in Berlin and his wife, Sarah Darwin, the great grand-daughter of Charles Darwin. As Sarah Darwin has just returned from the Galapagos Islands, where she has identified a new kind of tomato, the interview begins with a comparison of the world then, when her great-great grandfather sailed to South America in search of material for his 1857, The Origins of Species and the places he visited as they appear today. Like her husband, Sarah Darwin is a botanist and both are deeply concerned about the state of the environment and the half-hearted nature of the measures which are supposed to tackle the problem. Nevertheless, confirming the position taken at Reloading Humanism, although they see the situation as desperate in the extreme, they are optimists and know that there is no alternative but each and every day, to do what they can. With respect to the natural world, we must as Sarah Darwin says: „protect what is still intact and restore what has been lost“. In the Berlin Natural History Museum, climate change and defaunation are prominently addressed. Deploring the lack of knowledge that, when it comes to evolution, characterises most grown-ups, Vogel says: „How can we understand how bio-diversity is related to our survival as a species when we don’t understand the first thing about evolution?“ Accordingly, he has written a book on evolution for eight-year-olds. As at Reloading Humanism, not only does Sarah Darwin see education as being essential but also equally essential is a re-connecting with the good that is in each and every one of us. The interview thus confirms a number of tenets central to the Reloading Humanism initiative and so is encouraging. For the original interview in German conducted by Boris Herrmann, see: Nichts ist politischer als die Natur, in Suddeutsche Zeitung, Samstag/Sonntag 27./28. January, 2024, „Buch Zwei“, pp. 11-13.

Arriving in Saint Pölten I head for the Lower Austrian Theatre where Isabella Rossellini is billed to give a performance that was quickly sold-out. As the curtains draw back, the evening begins with a montage of clips from silent films, heavily laden with dramatic gestures and heart-felt expressions of emotion. This paves the way for an introduction to a later work by Sarah Darwin’s illustrious great grandfather, his less well-known work of 1874, The Expressions of the Emotions in Man and Animals. In this work, Darwin went on to argue that humans and animals are linked by a common heritage with there being an evolutionary continuum of shared emotions and gestures used to express them. Not only an actress and model, Isabella Rossellini has an M.A. in ethology and has always loved animals. Using a variety of ever-changing techniques, in a daring and staggeringly original one woman show, she introduces Darwin’s work on emotions in people and animals in a way that is by turns informative, witty, engaging and packed with surprise. Having introduced the idea that animals have emotions just like humans do and accordingly use a variety of facial expressions, gestures and behaviour to communicate them, the question then arises of which came first, the behaviour associated with an emotion or the emotion itself? Drawing on her experience as an actress and model, Rossellini explains how actors slink into their roles, with inner thoughts and external behaviour influencing each other. This in turn means that in acting, the circumstances of a performance also enter the picture and between the actor and his or her viewers, there is a rapport or empathy. In her scientific work, it is empathy in animals that Rossellini is interested in. Yet for science this is problematic as although empathetic behaviour can be identified, it cannot be measured. Nevertheless as Rossellini makes clear in a masterfully delivered form of bon mot with which she concludes the show, it is there and in the case of theatre, is what makes theatre theatre. Deservedly, Darwin’s Smile receives a standing ovation and whilst it demonstrates that art and science can be combined, it is important remember that Isabella Rossellini lives and loves both her acting and her scientific work. Apart from bringing love and decades of experience and reflection to bear upon her subject, she also brings an absolute mastery of the medium that she has chosen as a means of expression. Bravo!
Tips:
In Guy Maddin’s, The Saddest Music in the World (2003), Isabella Rossellini is the intoxicating and uttering engaging star in a bitter-sweet tale of a dysfunctional family in which father and son are both in love with the same woman and in which a competition is held to find the music that gives the film its title.

Reflecting her enthusiasm for biology, in 2009, Isabella Rossellini wrote and produced a series of short films:

In Meine Hühner und ich (2017) she celebrates her chickens with drawings by herself and photographs by Patrice Casanova.
2024, Week 6
At last returning to Parmenides, I see that the chapter on truth is badly in need of re-writing and break it into three separate chapters. This raises the question of „What would Parmenides‘ philosophy of mathematics been?“ with the work on continuity in the number series giving extra backing to the view that I slowly work out.

Despite influenza incapacitating a quarter of the guests, a successful Burns Night is held with a specially designed table ornament being made to mark the long planned and long awaited event. Dressing for the occasion, I wear a black jacket with the Reloading Humanism blazer badge, combined with a tartan bow tie and cummerbund made from a fabric which is now the Reloading Humanism tartan.

In order to endow the event the degree of ceremony that is its due, I wear a chain of office and act as Master of Ceremonies. From the metaphorical „chain“, which is in fact a ribbon, a glass ball is suspended. This is the Reloading Humanism, „Out of Itself“ burning glass ball, shown on the coat of arms.

After a toast made with Sekt or Austrian sparkling wine, the haggises (for there are two) are piped in. As the piper is among the flu victims, a recording of a fanfare of Roman trumpets accompanied by a water organ is used as a substitute. Where the first haggis was made according to a traditional recipe, the second was a vegetarian option, tried and tested three days before. This is followed by a lemon-flavored cheesecake moose, whilst to round the meal off, there is a single malt whisky from the Isle of Arran. In honour of Robert Burns, guests were requested to contribute something towards the evening’s entertainment. As Burns wrote in dialect and this sets the tone for what is to come. Contributions begin with a recording of Ernst Jandl’s sonnett Liedtext. This is read by the author to the accompaniment of saxophonist, Wolfgang Puschnig. Evocatively minimal, the words and letters, „The A, the E, the I, the O, the U“, are read slowly in a series of permutations that provides the basic units for an inkling of a new beginning. For the German text see: https:lyricstranslate.com. Appropriately, this expands upon the life-affirming Humanese, exclamation: „Soi-e-a-o-u“. There then follows, Der Bücherfreund, a wonderfully unapologetic homage, ode and hymn to books and the love of books written by Joachim Ringelnatz. See: www.gedichte.eu. Finally there is Michael Haas‘ Der Vierter König, with the theme of poetry in dialect reappearing in a humble and humorous narration, in which a tale is told of a fourth wise man along with the reason why he does not feature in the Bible narrative. For a brilliant rendition by Victor Gernot see: www.youtube.com. For the text see: filia.cc.
Mixing the qualities of gold, frankincense and myrrh and wanting to honour the Christ Child with something a little more heart-felt and less bombastic, Jiri Prihoda brings the Holy Family a speciality from his native Bohemia. This is quargel, a golden, semi-hard cheese that like frankincense and myrrh is transparent. Prompted by Ringelnatz, I search among my books and soon enough find what I am looking for. As discovered by the sixteen century alchemist, Bartholomäus Spangler, when repeatedly cooked, from quargel a form of artificial horn or plastic can be made and these early forms of plastic were seen as a great wonder. Perhaps there is more to the story of the Fourth Wise man than meets the eye!

I had thought of reading a poem in which the aims of the evening were to be announced but then decided against this. While the poem, being written specially for the occasion, was appropriate, I was unhappy at the thought of reading it in either English or German as through overuse and our heard-it-all-before cynicism, I felt the words were too slight and lacked the ring and weight of what I wanted to invoke. I thus resolve, over the course of the year, to translate my poem into Humanese, the language I am inventing in which I feel at home, where I can once again rejoice at the sounds of words and where there is neither cynicism nor rampant egoism. Once recited, a translation can then be given, with it no longer being important whether the translation sounds flat or weak, because what is important has already been said with the life and resonance of a fresh and un-corrupted language.
2024, Week 7
The week is spent working on Parmenides and finishing the Kouros sculpture begun a year ago. As the text written on the shoulders is too small, I write it again in much larger letters and seeing that this provides the missing element in an area where, despite the exaggerated muscles, not quite was enough happening, I immediately set about engraving.

As the sculpture is as large as a child, this makes me feel like a tattoo artist, a feeling that I am not entirely comfortable with. The text reads: A work that is a program, is in all our actions. All our actions are deeds. Happy with what results, I then set about making the piece weather-proof. This involves a coat of paint, followed by a layer of stick-on aluminum foil to which further layers of paint are applied.

Appropriately, during the week Susanna Fazun’s film, I Giacometti is screened at the Kesselhaus Kino. This introduces Giovanni Giacometti, an innovative turn of the century painter and his artistically talented children. Of the children, the eldest is Alberto, who like his father studied painting even though he is best known for his sculpture. Although Giacometti’s extruded, hugely condensed figures are a long way away from how I conceive of sculpture, I nevertheless get the message and see his work as embodying Heidegger’s concept of „Being-there“ and that we are „Beings-in-the-World“. Following Heidegger, we are first and foremost beings with an allotted span of time in which to live out our lives. Everywhere we go, with every step we take, we carry with us the knowledge that we will one day die. The question of what one is supposed to do with one’s life is thus set against an existential backdrop which if we do not block it out, informs everything we do. Whilst knowing what one is about and what one hopes to achieve in life is important, nevertheless one should not give too much of the limelight to the ego but should also let the unconscious self and its many concerns have a say. Only so can we live genuinely happy, balanced lives and know who we are.
Continuing these thoughts, although couched in the language child-development and the concerns of the young adult not yet become grown-up, I see that a model of self I developed two years ago, is not so much an interface between neuro-biology and geometry but instead is a mathematical sculpture whose true purpose is to inspire. On the model, from an infinitesimal point, projections are made that result in a sense of boundary arising between what we know and what we do not know, along with a vertical axis of good and bad. In the context of the search for happiness and answers to the question of who we are, it is important to emphasise that the model does not feature a self with a closed, sharply defined border but instead presents a self that encloses the whole of the world that it knows, whilst from the all-encompassing beyond that is not known, a sense of value arises. This makes us first and foremost ethical beings and ultimately I realise, the endeavor is an ethical endeavor. Against this background, Giacometti’s figures are a mid-point between the confidently rounded forms of my Kouros figure and the geometrical starting point of my model. Yet I feel that geometry alone, is not enough. Instead the geometry needs to be turned into meta-mathematics so that it might tell a story and articulate for itself who we are. Prompted by the films of the last weeks, after almost thirty years I return to Gödel, Escher Bach and conceive of a book that would be a mathematical, geometrical and sculptural fugue that would articulate my model of the self. To this effect it would dissolve the boundaries between art, mathematics and philosophy.
2024, Week 8
Re-reading Gödel, Escher Bach I see that there is material in it for my Parmenides book and during the week I formulate for Parmenides, an up to date philosophy of mathematics, integrating it into his philosophy of Being. I also work on the tricky notion of truth, re-reading Tarski. Beginning a small sculpture of Parmenides to use as a cover motif, I quickly see that the proposed design is getting fussy and over-complicated. Discussing the sketches with someone in publishing, we decide for something much simpler. Nevertheless, as the work has become something and is no longer just a sketch, I continue working on the figure.

2024, Week 9
The week sees not only the completion of the Parmenides manuscript but also of the Kouros figure for the garden.

The figure finally installed and the Parmenides manuscript being proof-read, I leave for the airport. On the flight, I work on my idea for a mathematical, geometrical and sculptural fugue that articulates my model of the self. This involves a series of sculptural reliefs involves distressed bits of wood, scrap metal and bits of rusty machines that I have been collecting over the years, repeatedly wondering what their purpose they are destined to serve.

Some of the material is in Stein, some in Scotland, whence I am heading.

The day after arrival, I am in my father’s workshop seeing whether the combinations I have in mind will work. Over the course of my stay, out of an old washboard and a shilling coin electric meter, I make a piece that ends up being 90% finished, with only the right-hand niche waiting for a dancing figure who has yet to made.

The point of this mix of mathematics, philosophy and art is from out of the dysfunctional scrapheap of modernism, to redefine the self in a way that is about the world as a whole and not about the differentiation of the self from things in the world.
2024, Week 10
With my father, I visit the Roman forts at Trimontium and Woden law. Trimontium was a sizeable military base with a permanent garrison of around 1,000 troops. Built on a naturally formed embankment, it occupies a commanding position that overlooks the River Tweed running immediately below. From 1905-1910, this was investigated by the Melrose solicitor and archaeologist James Curle, who was my great, great uncle. Together with his brother, Alexander Ormsden Curle, who was my great grandfather, the two brothers were an important driving force in Scottish archaeology. Although apart from fields of winter wheat, there is little to see of the complex, we walk around the extensive perimeter. Through walking and looking at the display boards, we get a feel for the site’s defensive position and can see why engineers over the ages repeatedly sited the bridges and fords at the point where they did. We also see the amphitheatre that provided entertainment. Behind the fort there are three hills known as The Eildons. These are the three hills that the Roman name refers to. Visible for miles around, the highest was a signalling station. Twenty-five Kilometres to the South, the next signalling station was Rubers Law, below which lies the Valley of the Rule where my grandfather and then I and my brothers would spend our holidays. From Trimontium, a Roman Road, leads in a straight line south-east. This is Dere Street which after twenty-five Kilometres, turns north a little before heading for the undulating Cheviot Hills. At a place a called Tow Ford, the road turns again and climbing up, passes the fort built on the top of Woden Law. Below, there are traces of a Roman camp. As the area between Hadrian’s Wall to the South and the Antonine Wall to the North was not always settled, passing troops and road builders would often enclose themselves in systems of quickly erected defensive walls. From Woden Law, Ruber’s Law and the Eildons are clearly visible and stand out amongst the otherwise gently undulating Border hills.
Leaving Roman history, two days later head south-west and return to Priesthaugh, visited in November of 2023. This time there is no fog and I climb up to Penchrise Pen where there was an Iron Age fort.

Along the way, I encounter a sentry box from the war, in which someone presumably stood, guarding who knows what.

From the top of Penchrise Pen, two valleys away towards the West, there is Skelfhill Pen.

To the north-east, just over 10 Kilometres away, there is Bonchester Hill and the Valley of the Rule where my father and brothers live. Seen from an enclosure two-thirds of the way up Bonchetster Hill, Penschrise Pen and Skelfhill Pen form a natural sight between which, on 7th February, the sun sets. The sight is further framed by the slope of the upper part of Bonchester Hill itself.

This suggests that as discussed in Week 49 of 2023, the enclosure is Neolithic and was sighted so as to indicate the mid-point between the winter solstice and the spring equinox (see also Week 47 of 2023). Lower down there is an circular enclosure with a ditch very similar to that on Bonchester Hill. Yet inside, there are hut circles. This makes the structure something very different to a Neolithic enclosure used for ritual purposes and underlines the importance of getting the site on Bonchester Hill dated. Happily my brother’s plans for a project in which a number of Border sites are to be dated through the taking of core samples is moving ahead. This involves volunteers being taught how to take samples by a likewise, voluntary teacher. The subsequent C-14 dating will then involve a lab and payments for which funding will be required. More news in September!
Having prepared four medium-sized tablets of wood and scrap for transport, on the flight back, I give a final polish to my thoughts on the intended series. The result is a concept and detailed plan for a series of eight reliefs, for which I must in addition engrave the coin designed in Week 33 of 2023.
2024, Week 11

Back in Stein I finish the fourth Wachau Audio Guide. This was to be entitled, In Vino Veritas but I change the title to Wine is Everything. Along with the motto, Wine is Over and Above Everything, this written onto the walls of the folly that was built over the entrance-way to the cellars of Dürnstein Abbey. Although the saying In Vino Veritas is well-known, the full meaning and history lying behind it and the other mottos is not and it is this lacuna that the guide is intended to address.

Meanwhile, since February Martin Gut has been working on the music for a choral piece. The libretto is my poem, The Artesian Well at Harty Ferry, which begins:
Since time I can remember
and other times long before,
the well at Harty Ferry
expunges hidden water
in a never-ending flow.
No water of a harmless,
and ever-babbling brook,
this water from underground
has wrestled the Weald’s clay,
percolated Downland chalk
and in the dark, time has whiled.
…
The time I can remember is a collusion of childhood memories, one of which is specific. After spending a night on the Swale in a yacht, the dogs needed, as was usual, to go ashore before breakfast. For such a short trip I did not bother getting dressed but went ashore in my red tartan pyjamas and walking up the hard in bare feet, came to the ever-spouting artesian well. The composition is for a competition which if won, will result in it being performed by a choir of four and at the end of the week the piece is submitted.
2024, Week 12
The week begins with my reading a book review of Nikolaj Schultz’s Land Sickness („Die Oma ist Schuld“ by Hilmar Klute in Suddeutsche Zeitung, Samstag/Sonntag 16./17. März 2024). This fictionalised travelogue on global warming is the reviewer finds, for the most part, „a tearful aria of accusation“. Amid „the narrations of guilt and hot-house heat“, there are however Klute finds, „two flashes of brilliance“. One relates to the need for, with respect to the environment, a new definition of class. With respect to the impending environmental catastrophe, the traditional class war is no longer relevant. What is relevant is the war and exploitation being conducted by people from all of the traditional classes on the environment. The other flash of brilliance is for Klute, the author’s seeing a human being as being composed on the one hand of water, air and molecules whilst on the other, it is precisely these that we emit. This results in a form of interference and an interface which, if a status quo is to be maintained, makes fighting for an intact environment essential. This Klute says, has the stuff necessary to replace Kant’s Categorical Imperative of Kant („act only according to that maxim whereby you can at the same time will that it should become a universal law“), with something which, although it does not know it, the environmental movement is in much need of. The problem is that Schultz’s post-modern tirade of introspective self-punishment, following in the tradition of Soeren Kierkegaard, is defeatist and gloomy. Over the last six years, this has been precisely my point! With my geometric-mathematical model of self, the aim is to provide a new way of seeing ourselves. To this effect, the article written two years ago and the planned series of sculptures, are but the beginning of a series of articulations intended for a wider reader and viewership. Accordingly the model must be presented in ways that are both understandable and inspiring. This of course is a tall order but so is solving the environmental crisis. As I have also always been saying, at bottom, the problem is one of culture, how we think and who we think we are. Were we to see ourselves differently, we would behave differently. This is why the environmental movement ought to concern itself with philosophy and needs a properly worked out conception of who we are and what we are supposed to achieve.
Over the course of the week I begin work on the first of the planned series of works conceived of in Scotland and work on the figure of the nearly finished eighth piece. Unhappy with the motto on the reverse of the coin designed in Week 33 of 2023 and which is essential to the last piece of the series, I change the motto from: „Find the balance, square the circle, reach for the stars“, to: „Find the balance, square the circle, care for the stars“.

Whilst the stars in themselves do not need caring for, the atmosphere through which we see them does and in China, there are no stars for the simple reason that they are veiled in smog. By referring to the health of the world as a whole and to Schultz’s interface, a moral imperative is generated in which we are active agents who are behoven to look after the environment we find ourselves in. Continuing these thoughts, I abandon the motto and repeatedly change the design. At first I draw from Parmenides and the dancing figure made for the El Très exhibition of 2023:

Then I return to chaos theory and the squared circle:

Then finally I arrive at what I am looking for and the modified motto returns:

Meanwhile Martin works on an unplaned composition prompted by a poem written by myself in Ancient Greek entitled „The Language of the Crucible“.
2024, 21st March
Spring has long been in the air with the daffodils in full bloom and tulips about to flower. Inaugerating the official beginning of spring, the eighteenth century candle on the console table in my hallway, is replaced by an ostrich egg. This is a symbol not only for Easter but also for the Celtic festival and season of Ostraca. Via the Old English and the German, „Osten“, the word „Easter“ derives from „Ostraca“.

As with Christmas, behind the date of Easter there is also a story. A moveable feast, or festival, Easter is celebrated on the Sunday after the first full moon of spring. As explained in the Wachau Audio Guide, „Wine is Everything“, early Christianity was very much a fusion of Church teaching and local paganism. During the Bronze Age, a dual system of time-keeping was followed in which both solar and lunar calendars were used. This is derived from analyses of artefacts and from a fragment of Greek mythology in which solar and lunar gods and goddesses contend for rulership of the sky. Following on from this, during the Iron Age, the Celts also used a highly sophisticaed lunar/solar calendar. The combined result of solar and lunar cycles, the date of Easter would thus seem to be an echo and relic of a dual system of time-keeping and an indication of how deeply entreched and difficult to erradicate, local pagan traditions were.
2024, Week 13
The „Wine is Everything“ Audio Guide finished, there still remains the task of drawing up a schematic map for the Dürnstein tour. Although this sounds simple, getting the right degree of detail (not too much, not too little) is tricky. For the guides to Krems and Stein I had used an old map bought for fifty Cents from a flea market. This made all the simplifications I needed and all I had to do was to trace out what I wanted and re-draw.

Nevertheless the endeavour had had a sting in the tail and in the process of tracing and re-drawing, my eye was caught by the designtion „NSDAP“.
Looking more closely, other telling details revealed themselves and I see not only where, in Krems, the National Socialist German Workers‘ Party had once had their headquarters but also that for seven years the Ring Road in Krems was called „Adolf Hitler Street“. This gives the map a date and a sudden twist to my supposedly innocent endeavours. With respect to a map of Dürnstein, neither the past nor the present is able to supply me with what I need and I am reduced to ham-handely tracing screen shots from the internet. From three A-4 sized tracings I then draw the much needed map. This shows the main tour in red, the two castles tour in yellow and the wine and saffron tour in purple.
After a year of intermittent struggles, another job brought to a successful conclusion is the re-writing of the introduction to the essay, One World Pragmatism. Here the difficulty was that of announcing what is being offered and of explaining what makes One World Pragmatism different from other forms of pragmatism. This sounds simple but in order to arrive at something, the need for it must first be identified and surrounded by trees, one often loses sight of the wood. Thus at the end of the short answer to Question 5 (Is the God capable of intervening in worldly affairs?) I write: „Leaving bone-head materialism behind, both modern logic and physics do appear to be capable of providing tentative and sketchy indications of how an interventionist divine principle might operate.“ This principle is of course God and it is and always has been our task to find him – using the tools, words and concepts of our age. This is why I was immediately at loggerheads with my sculptor tutors in Edinburgh – they did not like my searching for something higher as searching for something higher meant invoking thought and concepts and this was not desired. For them sculpture was about form and nothing more. Prompted by Douglas Hofstadter’s Gödel, Escher Bach, the series of sculptures concieved of in Scotland are a return to the questions that were besetting me back then and are an attempt to give God a form of telephone number and address. To this effect, I must combine art, philosophy and mathematics, so that dissolving the boundaries between them, from the scrap-heap of moderism, the divine and that which lies over and above us might be reached out to and called by a name that has been forged from the present instead of being blindly inherited from the past. Thus inspired, I crack on with the dancing figure for the last piece of the series. This is not an image God but of man filled with God and thus, following my model of the self and God, an image of man filled with the knowledge of chaos theory and the Morse-Thule number that, associated with the latter, reaches out to God.
2024, Good Friday
Over the week I read Aristophones‘ comedy, The Birds, in which the hoopoe bird plays a prominent role. While I appreciate the rauchous, fast-moving humour, it is only later that I realise that for me at leat, there is also a serious message.

A dancer dressed as a bird-man on a jug in the British Museum
Human beings are the chorus proclaims, „feeble, wingless creatures made of clay“, whilst birds, being airborne, are „un-aging and imperishable“ and have a far more superior pedigree. This is because in the beginning, there was nothing but Chaos, Night, black Erebus and dready Tartarus. In the boundless womb of Erebus, black-winged Night the laid the first egg. When the egg hatched, Eros sprang forth and mingling in murky Tartarus with Chaos, begot the race of birds. When they hatched, it was Eros who led them up towards the light. As the first born of Eros, it is the birds who are the true rulers of the sky and not Zeus and his later relatives. This account is substantited by fragments of Orphic mythology and is a garbled echo of the great goddess of the Neolithic. As expounded in the „Wine is Everything“ Audio Guide, the goddess of the Neolithic had many names and changed according to the seasons, becoming by turns bird, woman, snake and goddess of death. Appropriately, the story of the first egg and the birth of Eros feeds into the mathematical/philosophical series of scultures that I am working on as the first piece features an egg-like device with an inherent etension that is just waiting to explode.

2024, Holy Saturday
As I do every year, I buy a 20 Centimetre high hollow egg, which decorated and filled with things, is then an Easter present. This year, the only cardboard egg avilable is of such a displeasing and ugly shape that I buy a plastic egg with some kind of painting kit for children inside. When I get home, I find that the kit is an egg-painting kit with five plastic eggs enclosed. As throwing the plastic eggs away is a waste, I take a cue from Aristophones and adorn the five extra eggs with motif’s inspired by the creation myth given in The Birds.
2024, Easter Sunday






2024, Week 14

Not making blog-line news, „Parmenides“ has nevertheless been ticking away in the background. Proof-read and with the corrections typed in, I make an important change to a Latin word square that I devised thirty-nine years ago in Edinburgh. This was the conceptual underpinnning of a sculpture, which needless to say, caused a frowns among my tutors in the sculpture departement. In the book on Parmenides the word square occurs as an illustration of Heraclitus‘ view of the world, which I then contrast with the view of Parmenides. In the original version, the square was composed of the words „Logos, omnia, gnare, omnes sesse“. This means „Logos, the One thinks All to Itself“ with the middle „s“ of „sese“ (itself) being made into a double-S so as to fill the square.

Yet I realise that if the ambition of making a word square is abandoned and the 24 letters are made into a sliding-letter puzzle then, not only is the word „sese“ uncorrupted but the enpty space that is necessary for the letters to be moved around, becomes laden philosophical significance. This is because if the world is „full“ (as Parmenides argued it was) then there is no room for anything to move and accordingly there can be neither change nor movement. Yet if, as the first atomists argued, the notion of empty space is introduced, then movement is possible and things can change from one thing into another.

I also solve a layout problem, working out how a loose and lively translation of the surviving fragments of Parmenides‘ philosophical poem can be combined with interpolations in a way that enables the whole to be easily read whilst it remains clear which passages are interpolated and which are translated.
After the explosive egg, the second work in my intended series thematises the void and the notion of empty space. In Plato’s Timaeus space is „the mothering nurse of all generation“. Both the wooden background and the rusty iron bar on the right-hand side of the piece are from the debris of an abandoned mine in the Lake District. Found twelve years ago, after being combined, they then bided their time in the darkness of a store-room in Scotland and have only now found their calling.

2024, Week 15
As the Venus of Willendorf and associated paper model are essential to the website, I find it problematic that the model is not available for people to buy. Not wanting to set up and run an internet shop, I decide to solve the problem by publishing a print on demand guide on the Venus with the paper model enclosed at the end. To this effect, before the first Reloading Humanism Guide is even finished, I am hard at work writing the next. This is in any case a long harboured aim: filling the gaping void created by the fact that on Austria’s most famous artefact there is and has never been any form of genuinely informative guide.
2024, Week 16
Jumping between the covers and content of the Venus of Willendorf guide and the Parmenides and Sappho book, I finalise the design for the covers of both and thus for the series as a whole. This includes the blurb paragraphs for Parmenides, Sappho as well as for the series in general.

As the week progresses I come to the conclusion that all Reloading Humanism Guides, even the short ones such as the Venus of Willendorf guide are to have footnotes. This is unusual but necessary, both for the sake of exactitude in itself and in order to send out clear signals of reliability and assurance. After a trip to Vienna I return with gold paint and the week ends with the completion of the third sculpture of the new series.

2024, Week 17
Passing a junk shop in Stein, I see a bronze patinated sculpture of a woman playing a lyre and immediately know that it is the centre-piece for the 2025 Burns night. As it is damaged, the piece is affordable and the next day, I am the happy owner of Émile Bruchon’s, Le Réveil des Oiseaux. As the sculpture lacks a base, the idea is to make one in which a device is contained which plays the music that awakens the birds. Ideally the music would be given by a circle divided into 15° segments with the 13,14,15 triangle indicating, as described in Week 5, a theme. But for this I must wait for Martin to see if he can come up with anything.

2024, Week 18
Working on the Venus guide, I find the material telling me to go in a different direction to the one worked out in Week 16. As new insights come thick and fast, I abandon the poppy comic look of the cover in favour for something more serious.

Happily I find philosophy sneeking its way in with modern genetics providing a plausible explaination of why there should be a link between Gravettian Venus figurines and the concept of truth articulated by Parmenides thousands and thousands years later. In the art historical analysis, making a copy of the Venus of Hohle Fels provides new support for what I am saying and suddenly I find everything falling into place in ways that I had never even dared contemplate.
2024, Week 19
After uploading the Parmenides and Sappho book at the Buchschmiede, I mark the Celtic festival of Beltane by changing the object on my console table and am rewarded with an inspiring image of spring in full flush.

Reading Amitav Ghosh’s The Great Derangement, I at last find confirmation of my views concerning contemporary culture. In his book, Ghosh takes contemporary literature, history and politics to task. Although this trio does not include contempory art, everything Ghosh says can be applied to the art world. Summarising in a few lines, contemporary culture is nothing but a facade of lies whose purpose is to preserve the status quo. As Ghosh obeserves, the status quo is a system of power that is based on the consumption of fossil fuel. Thus, while the idea and necessity of change is not denied, in practice nothing is ever done that will unduly rock the boat of those currently in power. Thus at bottom, anyone who is either passively or actively involved is a collaborator who hinders and down-plays our ability to appreciate the danger that climate change is putting us in. It is thus highly ironic (and dis-heartening) that of all the arts, literature is the best placed to address the what-if situations of future scenarios and to prompt discussions on how we see life in the future being lived. Yet here as elsewhere, there is a blind clinging to a form of social realism that keeps the focus firmly on the present.
2024, Week 20
As work proceeds on the Venus of Willendorf book (the word booklet is no longer appropriate), I perceive that the diverse nature of the graphics requires me to embrace new directions and trying out ideas, I am relieved to see that what I am contemplating will work.
Returning to the idea of a CD of music composed in Krems, conceived of in Week 2, I find a number of scores available on-line. Others I order from the National Library in Vienna whilst a last musical fragment written by Beethoven whilst staying with his brother just outside Krems, I find on YouTube. This I am happy to note, is easy to approach and despite only being a fragment, has an infectious quality. As it is the beginning of a piece, it makes musical sense to use it as the first work of the CD, with the sudden stop announcing a journey back in time. Here the question is: „How far back in time?“ As far as sheet music is concerned, I have material that goes back to the sixteenth century and proceeds from there to link up with the era of Beethoven. Going back further is possible if one allows music to be included that is inferred from instruments found in Krems but this compromises the clarity of the concept: „composed in Krems“ and so I decide that in the first instance, it is the period from 1563-1826 that is to concentrated upon.
2024, Weeks 21, 22, 23
As the weeks go by, while the order for a mock-up proof of the Parmenides and Sappho book disappears in digital Nivarna, the Venus book edges its way towards completion. One after the other, content and graphic problems are solved and I even succeed in integrating the paper model into the main text as a content element with a narrative function. This is infinitely preferable to its being a form of a castaway, unwontedly consigned to the netherworld an appendix. The summation of 20 years of research and thinking about the Venus of Willendorf and 30 years of thinking about art, the work fuses archaeology, art history and philosophy and is a form of sculptural/existentialist statement.
2024, Week 24

In between drawing maps and the last remaining images for the Venus book, I tidy up the workshop and resume work on the series of mathematical/mechanical relief’s started in Scotland. At the same time, Martin records a piece inspired by my poem, The Language of the Crucible. An ode to alchemy and all process of distillation and sublimation, the poem praises the hidden value of slag and dross and after six months of philosophy and art history, I feel the urge to sit down and work out the mathematics that the blank boards and rusty bits of metal are crying out for. This is nothing other than the metaphorical address (and telephone number) of God.

2024, Week 25
The proof of Parmenides/Sappho arrives. Three mistakes are found and some minor but significant improvements are made to the cover.

As the work is part of a series of Reloading Humanism Guides, the cover must be adaptable to for future works so that in order to finish the Parmenides cover, I must also finish the Venus of Willendorf cover.

On my console table, the emblem for spring is replaced by an image of summer and on the day of the summer solstice, work on the internal layout of the Venus book begins.

2024, Week 26
In order to introduce the Venus of Willendorf I not only need a theory of art but must also explain why human beings respond to the proportion known as the Golden Section. This involves going back to the very beginnings of the human story.

As the week develops, I finalise a series of photomontages featuring the four most prominent of our ancestors: Dryopithicus, Australopithicus, Homo erectus and Homo neanderthalis.

Over the last twenty years, plastic figures of these pesonsges have formed a cheerful crew that has accompanied me hither and thither, moving around the various districts of Vienna and then to Krems but never quite fitting in when I requisition them.

At last finding their places, in the book they are important as apart from standing as examples of our forefathers of long ago, they also provide a touch of irony that serves as a reminder that anything we say about the past is a matter of conjecture and speculation.

2024, Week 27
At long last Parmenides/Sappho is available at www.buchschmiede.at! Setting up a link on the Reloading Humanism Books and Music page, I place an order for 49 copies for personal distrubition. Although I would like to work on the maths behind the series of sculptures begun in Scotland, I realise that Piero della Francesca is the more pressing priority and accordingly to re-write two articles for academic journals. This done, I jump back and forth between the Venus book and a third book: Art and Mathematics in Krems, the Wachau and Borgo Sansepolcro, with the articles anticipating some of the material. Writing cover texts and making mock-ups for both this and the Venus book confirms that this is indeed the direction in which Reloading Humanism is meant to be going and that things are finally falling into place.

Continuing the bibliophile theme the week ends with a trip across the river and a visit to new a bookshop in Furth-Palt. This is at the foot of the hill on which the monastery of Göttweig is perched and so is called buch am berg or „book by hill“: www.buchamberg.at. Run by Conni and Hubert Hladej, the small shop is stocked with a carefully selected choice of books from a number of genres, including high brow literature, easy reading literature, crime, reference books and childrens‘ books. Despite only opening three weeks ago, locals have already realised the advantages of a local bookstore. Open on Fridays and Saturdays, trade is supplimented by readings and events in schools, libraries and other locations. Climbing up the hill to the monastery, I take part in a tour of the Music Archieve at Göttweig. This is housed in an octagonal tower with turquoise walls that is not usually open to the public. For book-lovers, the atmosphere is entrancing and I find a motif for the cover of the CD of music in Krems, Stein and Göttweig. This is a cherub playing a zink, a zink being an early form of flute. While the monastery restaurant resonates vapid chic and fails to fulfill its pretensions, below in Futh-Palt the bakery/café has excellent cakes and is local and authentic.

2024, Week 28
External confirmation that the Venus book is important comes in the form of a new book by Philipp Blom. Aufklärung in Zeiten der Verdunkelung or „Enlightenment in Times of Darkness“, is the fifth book in the series, „To the Point“, published by former Finance Minister and Vice-Chancellor of Austria, Hannes Androsch: brandstaetterverlag.at. In this work, Blom argues that if the most important achievements of the Enlightenment (democracy, human rights and fact-based thinking) are to be preseved, then a way of life must be developed in which human contentment and environmental justice are paramount. Freedom Blom points out, is a two-edged sword for there is always the question of freedom for who and at whose and what cost. The same goes for equality and how the paraphrase, „All men are equal but some are more equal than others“ is implimentated by those with manipulative skills that must constantly be held in check. To this effect, Blom argues that human rights must be grounded on and bounded by, the needs of the eco-systems on which all our lives depend. He thus takes up the argument that natural entities such as rivers, should be accorded legal status. This is already the case in Canada and New Zealand and is so that when such an entity is polluted or otherwise abused, people may, on behalf of the entity concerned, bring a case against the perpetrator. In this way, a legal mechanism may be installed to teach us to work with nature instead of working against it. To this effect, Blom concludes by saying that we desperately need a new narrative of who we are and what we are about and this is precisely where The Venus of Willendorf and the Culture of the Gravette fits in. Hopefully available via the Buchschmiede in September!
During the week, Martin receives the video of his monchord performance of The Language of the Crucible, a poem I wrote in Ancient Greek some ten years ago. The video is intended as an introduction to his electric monochord, or Scheidt: brennstein.at. Despite the carefully stage white cube visuals, the poem together with a translation are to be available in the same window as the video. To this effect I supply the poem and translation along with images of slag and dross found in Cornwall and the Lake District. Paraphrasing, the poem concludes:
„Generated in fate’s mill, the stones and ores which we find beneath the ground, are not raw materials of no significance, with no message contained for us but token and betoken, pointing silently to that awesome drama that was this earth’s beginning. In a crucible, melting out the metal from nuggests extracted below the ground leads this process one stage on.“

„The slag and dross that thereby result are not mere products of waste without import but in truth are really words – words of a language spoken by things in times now long gone. Is it not time for us to try and decipher them?“

Weeks 29-32
As the text of the Venus book edges its way towards completion, my editor voices concerns that the photomontages of Dryopithicus, Australopithicus, Homo erectus and Homo neanderthalis are too much out of sync with the illustrations in the rest of the book, with the playful tone undermining the seriousness of the undertaking as a whole.

Consulting with other professionals in the field, results in mixed opinions and as I can see both points of view, I decide that I should experiment with doing my own drawings before making a decision. Drawing an australopithecine, I feel uncomfortable with the results and the next morning I awake with a number of different solutions, one of which I implement and making a print-out immediately see that this is the solution.

This subtly introduces „The Crew“ so that when they appear individually in subsequent pages the reader no longer experiences a visual shock. Also questioned is an image of a Gravettian woman holding out a paper model of the Venus of Willendorf. This was to have been a visual bon mot but as it competes with the paper model itself which is also a form of concluding bon mot, the image of a woman with her hair contained in a snoot of woven plant fibres is axed.

Meanwhile Art and Mathematics… proceeds by leaps and bounds and I find myself jumping about between two projects.
The Venus of Willendorf was found on 7th August, 1908 and on the 116th anniversary of her being found, on the console table that bears emblems of the eight Celtic seasons, as planned I replace the image of the sun with a replica of the Venus of Willendorf. This is intended as the image that inaugerates the harvest season.

Immediately however, I see that something is wrong and that Gravettian Venus figurines were never meant for prominent display in this manner. Accordingly, after less than a day in the sun, she is returned to the box where she resides. Then I desperately search for an emblem of the harvest that is not overloaded with clichéd symbolism. This it turns out, is a tall order, nevertheless, looking at images of corn dollies, I see a cornucopia and realise that a cornucopia, or horn of plenty, was originally a literal horn. This I fits perfectly with the Neolithic symbolism of the bull, which is a male/female symbol of the corn and the harvest. During the Neolithic, when the sun rose at the beginning of spring, it did so in the constellation of Taurus which after the winter, was just beginning to appear in the night sky. At the beginning of August the constellation would then sink back below the horizon, so that for these reasons, the bull was associated with the corn and the harvest and was celebrated at harvest festivals. On my console table, this makes a suitably presented horn the perfect emblem for the harvest season.

Week 33-35
My editor busy with other commitments, as I wait for the final edit of the Venus book, I take on a third project and prepare the manuscript of Rediscovering History in Krems and the Wachau for publication as a Reloading Humanism Guide. Work proceeds apace and the project quickly overtakes Art and Mathematics... For both books however, the statue in Museum Krems, Saint Vitus in a Vat, needs to be investigated in order to verify that the original ground plan was a 13,14,15 triangle. This however can only be done during the winter when the museum is closed.

On 25th August, in the Ursula Chapel in Krems, the 2024 microtonal music festival, Am Sound, opens with the 4×4, 4-Lined poems of the Persian poet, Rumi, being performed to music by Werner Schulze. This is followed by two songs in catalonian by Ramon Lull. Hildegard von Bingen’s Ordo Virtutum then concludes the evening with renowned musicians and singers receiving raptous applause from a full house.

The Venus book edited and with corrections double-checked, the layout prompts the incorporation of a photograph to show just how snugly the figurine fits into the palm of a partially open hand. Clearly meant to be held, the Venus of Willendorf was never intended for enclosure behind shock-resistant glass and the photograph re-iterates the significance and role of the cut-out paper model that follows.

The next day the book is uploaded and a proof is ordered from the Book Smithy while I return to Art and Mathematics… and Rediscovering History…
Week 36
In my library, my grandmother’s books on prehistory, are at last united with my own ever-growing collection.

These include an early publication in which the Venus of Willendorf is shown as the only work honored with a photograph as opposed to a line drawing.

Among the books and my grandmother’s notes, there are also artefacts such as a copy of the Bronze Liver of Piacenza that I made many years ago. This is an Etruscan model of a sheep’s liver, with the organ divided up according to the houses of gods who abide in the various regions.

Resuming work on the series of sculptures begun in Scotland, I complete another panel and see that the mathematical-sculptural undertaking is as intended, nothing other than a search for God and that by plodding along patiently I might be able to avoid the short-comings of Douglas Hoffstadter in his Gödel, Escher, Bach. Whilst admirable and impressive, Hofstadter’s undertaking is sadly let down by the quality of the dialogues, the cerebral nature of Escher’s work and despite the sporadic presence of Bach, the lack of something convincingly artistic or musical that is a continuous presence throughout the work and which compliments the mathematics in a manner that is comparable to what Hofstadter otherwise achieves. In my undertaking, I also have some mathematical friends. These are however, not just mathematicians but are also philosophers and theologians: Plato and Cusanus and the artist Piero della Francesca.

As I reorganize the chapters of Rediscovering History… the cover also becomes finalized with the porthole cover:

being replaced by something less distracted:

Prompted by the sight of Émile Bruchon’s Le Réveil des Oiseaux gathering dust in my workshop, my thoughts return to the puzzle I set Martin in Week 5.

Realising that he has forgotten about it and that the task of identifying a possible scale among the alignments that define the dates of the Reloading Humanism Burns Night is in fact ridiculously simple, I sit myself, sketchbook in hand, in front of a piano. With a circle divided into 24 15° intervals so that 30° = one half tone and with the upper corner of an equilateral triangle denoting C and the lower corners E and Gis, the lower corners of the equilateral triangle when connected by straight lines that run through the centre of the circle, on the otherside of the circle denote the notes D and B. The four notes thus marked out by the triangle enclosed in a circle are the points on the horizon where the sun rises and sets at the times of the summer and winter solstices when the top corner of a 13,14,15 triangle (likewise contained within the circle and with the side 14 units long forming the base and being identical with the lower side of the equilateral triangle) is aligned North. Here the 13,14,15 triangle is approximated to by shifting the upper corner of the equilateral triangle 15° East. Playing the notes D, E, Gis, B, in ascending and descending order results in the Phrygian scale which is in itself satisfying, musically appropriate to the theme of the year and its cycles and in addition invites the beginning of a melody, D, E, Gis, B, / B, Gis, E, D / D, E, D, E / E, Gis , B, D / …
Weeks 36 & 37
Having found a scale and the beginnings of a melody that derives from the 13,14,15 triangle, I return to the method I have devised of constructing the triangle from an equilateral triangle. This results in a triangle that is fractionally larger than the circle that contains the equilateral triangle.

This however is an approximation and so I devise another method but I then want to know whether it too is an approximation or whether I can prove that it is exact. To this effect I spend a number of hours trying out various approaches before realising that my various assumptions are correct and that the matter is actually incrediably simple. The construction method is however once again an approximation but this time with a very small margin of error.

Thereafter, using the top of the triangle as a pointer that indicates North, the eastern corner designates the direction of the rising sun on 3rd February while the western corner points to the place on the skyline where on 25th January the sun sets. From these points, by drawing lines through the center, the directions of the sun as it rises and sets on the day of the summer solstice may then be ascertained.

Diving the circle up into 24 equally spaced divisions enables one to construct an approximation of a 13,14,15 triangle. Using the 24 divisions, the notes of an equally tempered octave can be assigned starting at C which is one division away from the top of the approximate 13,14,15 triangle. The notes E and Gis then sound the points at which the sun sets on 3rd February and 3rd November, while D and B announce the rising and setting points on the day of the Summer solstice. The four notes together for the of the notes of the Phrygian scale.

This leaves the rising and setting of the sun on the day of the winter solstice unaccounted for. Yet the difference between the 13,14,15 triangle and its approximation gives the amount by which these points differ from the halftones that follow and precede E and Gis.

This provides a geometrically self-contained system to be constructed that relates the rising and setting of the sun to a number of significant points on the horizon. Around this, a story can then be woven, from out of which rituals such as a Burns Night can be concocted. While this is emotionally satisfying and stills a need for placing and orientating myself in the world and in time, like Christianity and the old religons, it can only partially be squared with a scientific view of the world and modern belief. What I am endeavouring with the new series of sculptures is to construct something that will underpin the web of geometry I have woven around the Steiner Kreuzberg. Nevertheless, the point is not to give extra support to what I have devised but rather to show that behind, below and beyond it and all such mythologies, religons and ritualised ways of interacting with the world, there is for us moderns, a deeper and more fundamental, underlying level. Whilst underlying the old, this other level does not however render the old superflous and this indeed is the crux. We need both. Where my geometrical constructions weave webs of whole number patterns around a circle that then enables the telling of simple stories, that which underlies the patterns and the stories, is more abstract and involves abstruse matters of number theory. Although abstruse, this is something that nevertheless needs to be articulated and given a face, a face that whilst underling and going beyond the simpler images of the past also enriches them, giving them renewed validity and vitality. Realising this, reaffirms my feeling that the endeavour I have undertaken is a multi-pronged assault on the emotional, cultural and spiritual void that modernism has not only engendered but is incapable of finding a way out of.
Bringing the summer to an abrupt end, four days of continous rain causes temperatures to drop and in Lower Austria there are massive problems with flooding. In Stein, although the Danube rises and the posts for the town’s flood protection wall are set up, the inbetween boading is not inserted and the river does rise to an extent that would make completeing the wall necessary. Nevertheless elsewhere, cars are washed away, people must be evacuated and a state of emergency is declared. Prevented from feeding by the heavy rain, exhausted housemartins fly whenever the rain eases, using up their last reserves of energy in a desperate bid top stay alive. Yet only a few survive and every morning the street is littered with bodies. The rain is evaporated sea water from an overheated Mediterreanean and so is a textbook case of the effects of global warming, with devastation and suffering being caused by too much water in the wrong place at the wrong time.
Week 38
My mind at last freed from conceptual worries concerning the 13,14,15 triangle, I return to the unfinished series of mathematical sculptures and again find myself beset with doubt. Rethinking the mathematical concept, I return to a box of tricks I developed a year and a half ago and spend the week wrestling with the contents. Just as I am beginning to despair, persistance pays off and understanding dawns. The half-finished tablet of week 24 finds its place in the series and I realise that my feeling that a figure is needed, is correct. The figure is to hold a tablet which announces the next tablet in the series. This then gives the beginnings of the maths and geometry that is a symbolic model of how, out of the multiverse, the world we live in and we ourselves came to be. Far from everything being cut and dried, despite being formulated in the language of mathematics, this is however a statement of belief that for the mathematically inclined, is a religious credo. The tablet thus outlines a program of research with results that probably lie far away in a future that may not even come. While the aim is nothing other than the discerning and sifting out of an address and telephone number for God, this is an aim that, if it is to be believed in as an article of faith that involves not only a thinking mind but also a feeling soul and a beating heart, then it must have something open ended about it that can only be believed in and which in the present at least, transcends proof. This indeed is the crux of the matter, for while I have the mathematical addresses for God arrived at by Plato, Cusanus and Piero della Francesca, whilst still magical and inspiring, they have obviously been overtaken by modern mathematics and the void they once so successsfully filled has moved on and must now be be filled in new ways.
Concluding the week is the autumn equinox and on my console table, as an emblem of the ending harvest season I place a barrel which stands for the wine harvest and the gathering in of autumnal fruits, nuts and berries.

Week 39
The week begins with my proof-reading the long awaited Venus book. Happy both with the choice of paper and the impression of the whole, there are however plenty of mistakes and for printing at the Book Smithy, some colour adjustments are necessary.
Reading Michio Kaku’s, Quantum Supremacy, I return to questions of 25 years ago and re-read John Gribbin’s Schroedinger’s Kittens. In this book Gribbin makes it clear that the Copenhagen Interpretation of Schroedinger’s equations is only an interpretation. This was was boxed through by Niels Bohr who with a strong personality, seldom lost an argument. According to this interpretation, whether a photon of light passing through a slit is a particle or as a wave is something that is inherently ambivilent and only decided when a viewer conducts an experiment that forces a decision to be made. This introduces an alarming degree of subjectivity that clashes with common sense. Equally unsettling is the theory proposed by John Everett according to which, each ambivilance is resolved in however many ways are possible. This means nothing less than that at each moment of decision, the world splits into two or more different versions of itself, with one version continuing on into the future with the one alternative whilst the other reaps the consequences of the other alternative. Whilst this removes the subjectivity of the observer that characterises the Copenhagen Interpretation, it results in there being an infinite host of worlds that are continually splitting into ever more worlds and so is equally absurd. Since doing A-Level physics at school, I have always known that the common sense attitude must be to accept that we don’t know everything there is to know about the physical world and that there may well come a time when new discoveries change our take on things and cast the dilemma of quantum uncertainty in a completely different light. Although such theories are at present lacking, what is indisputable is that 75% of the mass of the universe is completely unaccounted for. The philosophy of One World Pragmatism further suggests that as yet unknown masses/energies interacting with themselves as self-referential systems, may one day be able to explain a wide range of quantum phenonenon. By self-referential, processes are meant whose results feed back into themselves. With appropiate inputs of energy, such systems become dynamic and behave in ways that are radically different to linear systems. This raises the possibility that quantum phenomena might one day be explainable in terms of chaos theory, with quantum packets of energy being the stable points of an as yet undiscovered dynamic process. In his book, Gribbin also makes it clear that no one has seen atom with their own eyes and that the existence of all particles such as electrons, protons and neutrons are inferred. Whilst there is no reason to doubt the existence of these entities, it must be remembered that smaller entities, such as quarks, are very much working hypotheses. Gribbin further observes that the only unquestionable message that can be drawn of quantum physics is that if we want to subscribe to a common sense view of the world, then we must accept that there is „spooky action at a distance“. This means that a particle on one side of the universe is somehow linked to a particle on the other. Whilst strange, this is not absurd and when Newton first proposed the force of gravity it was also seen as spooky. This reiterates the fact that whilst common sense has its place, it is a reaction and conditioning caused by the linear world of Newtonian physics and so has not prepared us for worlds and systems which are dynamic and non-linear. As the Austrian-British philosopher, Sir Karl Popper said, although in general common sense should be defended against absurd theories and unnecessarily wacky claims, zones where common sense breaks down are to be expected and it is precisely here, when common sense is challenged, that things get interesting. The interconnectedness of all things at a quantum level, re-iterates the old truth that all things are one and inter-related and it is precisely this truth that we must bring back into our lives and understanding of the world if we are to have a future.
Week 40
The colour issues of the Venus book attended to, the manuscript of Rediscovering History in Krems and the Wachau enters its final stage prior to layout and reading the one remaining source book and watching a CD of the restoration of the Saint Vitus sculpture, I gain some valuable insights and prepare a pdf for a pre-layout read. The CD reveals that originally the beret worn by Saint Vitus was red. During the Renaissance, a red beret was an indication that the wearer was someone of learning and erudition and this accords perfectly with my theory that, on the ground, the legs of the cauldron in which the saint sits, describe a 13,14,15 triangle, with this latter being a symbolic secret that was only known to the burgesses who ran Krems. In November, Museum Krems will close for the winter and I taking measurements, I will be able to put my theory to the test.
Week 41
During the week I travel up and down the Wachau, taking photographs for Rediscovering… I also journey across the river to Göttweig and climbing the hill, head South, away from the monastery up towards the hill’s real summit. Here there are the remains of a church dedicated to Saint George. During the eleventh century, this was where Ava of Göttweig lived as a willingly interned, „prisoner of Christ“. Walled up in one of a number of cells that were built around the apsis of a church, during the Middle Ages numerous people willingly renounced their freedom so that through confinement, they might find new ways of communing with God. Although now only the foundations of the church remain, from contemporary accounts it is known that each cell will have had three windows. One window was for light, one was for food and conversation, whilst the third looked into the apsis of the church and enabled Holy Communion to be both participated in and received. In Ava’s case, instead of meditating and having visions, the former wife and mother, wrote on the life of Christ, rendering for the first time passages from The Bible into Middle High German. For Rediscovering…, I have translated three passages of Ava’s verses and given an outline of her achievements. In order to finish the chapter, all I need is a photograph of where she spent her last years. Happily sun and clouds oblige and I am furnished with the image I need.

Week 42
The religious theme continuing, I find out that in the library of the former Dominican Monastery in Krems, there was once a magnificent illuminated Bible. The library was above the entrance to the monastery and originally had a vaulted ceiling so as to make the space as fire-proof as possible. Today the space is the reception area of the Krems Bücherei which is the town’s public lending library. Although the old books are no longer there, the fragments of painted scrolls on the walls indicate where commentaries on the Old and New Testaments once were (South and North walls respectively) and above the entrance, an exhortation appeals to monks to value their time in the monastery and treasure the contemplative life that they lead.

During the sixteenth century, the precious codex known as the Krems Bible (ÖNB Codex 1174), was acquired by the Emperor and was transferred to the Imperial Library in Vienna. Hidden in the illuminated „I“ that begins the work, there is an image that perfectly illustrates something I discuss in Rediscovering History.

After showing the first six days of creation, after the creation of Adam, instead of showing God resting on the seventh day, the illumination jumps to the Temptation, implying the inevitability of The Fall and an innate flawed sinfullness. The miniture thus illustrates the Catholic doctrine of the Inherited Sin with which we at birth all afflicted and tarnished. In order to avoid copyright problems, this and two images from other manuscripts, must be copied on vellum. In addition, I must copy two printed pages and three sculptures.
Weeks 43-45

On my console table, the 5th of November sees the barrel of the autumn harvest being replaced by an hour glass. This was the day when, supposely Plato was born and both died and on the hour glass there is an engraving Old Father Time.

Finding a piece of vellum, I scrape off the ink of a poem I am no longer happy with and reuse the parchment for a copy of the beginning of the Melk manuscript of the Venerable Bede’s De temprum ratione.

Returning to Art and Mathematics in Krems and the Wachau, I decide to incorporate a translation of Cusanus‘ De quadratura circuli as an appendix. As my translation from the Latin is not up to scratch, I translate into English, a German translation that I only found once I had completed my own deeply flawed and highly imperfect translation from the original Latin.
Week 46
Not forgetting the Neolithic enclosure on Bonchester Hill in the far-off Scottish Borders I had asked my brother to photograph the setting sunset on 6th November, only for several days the sky was clouded over and so it is not until the 11th Novemember that he is able to scamper up and catch the sun as it sets. As with my other images this is a bit off from the two hills between which on 6th February and 6th November the sun sets, nevertheless it gives a good indication of what would happen on 6th November were clear skies to prevail.

From the centre of the enclosure, this is the last time the setting sun will be seen until February, as for the rest of November and the whole of December and January, all other sunsets take place out of sight behind the slope of Bonchester Hill (sloping in the above, from left to right). The hill thus marks out the winter period with the sunset between the two hills, indicating the dates of Imbolc at the beginning of February and Samhain at the beginning of November. Contining the Neolithic theme I finish my copy of the Bird Goddess of Melk and begin copying the Lady Toad of Maissau: uhasammlung.univie.ac.at.
Reading Joachim Bauer’s Feeling What the World Feels (Fühlen, was die Welt fühlt) I find the two-fold approach taken at Reloading Humanism confirmed. In this book (unfortunately only available in German), the acclaimed author and neurobiologist explains how empathy in a child is brought into being. This takes place through a loving environment in which the child leans that there are people around it who are happy that it is has arrived among them. This enables the child to empathise not only with others but also with the natural world and other living things. Although of crucial importance for the emergence of emotionally independent and mature adults, this facility has been massively erroded and undermined through social media, which whilst promising social contact, at the end of the day, fails to deliver. Observing that in our lives, both in the real world and in virtual worlds, we all tap into various forms of identity, Bauer sees the way out of our current dilemmas as consisting in the adoption of a global identity combined with a regional/local identity. This is exactly the stratergy taken at Reloading Humanism where a global identity is sketched out on the people page and complimented by the regional approach taken on the Mission page. In today’s world, Bauer sees people as being unduly obsessed with the question of what society says they are worth, as opposed to addressing the real question of who they are and what it is that they really want in life. This coincides with my analysis of the Venus of Willendorf and her Gravettian sisters, which I see as being concerned with finding answers to the question of who we are, where we come from and where we are going. Thus at Reloading Humanism, the Venus of Willendorf is a matriarchal figure and mascot who, along with a male cohort, the Krems statue of Saint Vitus in a Vat, prompts and reminds us that it is high time that we resumed this quest.
In the light of the above, it is appropriate that mid-week, I recieve news that the Venus of Willendorf and the Culture of the Gravette has been uploaded is available from the Book Smithy: www.buchschmiede.at.
Week 47
In Sind wir Menschen noch zu retten? (Are we Humans Saveable? – again unfortunately available in German), the acclaimed biologist and wolf researcher, Kurt Kotrschal, argues that neuro-biological models of what a human being is should integrated into all areas of law, replacing ideologically burdened models that fail to take into account the realities of who we really are. This is in accord the view of Liza Herzog and other ecconomists, that the Homo oeconomicus model of what a human being is is an absurd abstraction that has nothing to do with real people and their motivations for doing things. In his warts and all analysis of who we are, Kotrschal argues that only liberal democracies are capable of addressing the long list of problems that the world faces. Like Bauer he sees social media as a major cause of many of the world’s problems and of our voting for poularist leaders who are a major threat to democracy and the urgent need that we address the problems of climate change and defaunation. Kotrschal also sees people as being alienated from their own inner feelings through an over exposure to social media with this constituing a major hurdle to finding out who we really are, this being a question which, like Jochim Bauer, he sees as being hugely important.
Continuing this unhappy theme I read in Bun Chul Han’s Die Geist der Hoffnung wieder die Gesellschaft der Angst (The Spirit of Hope against the Society of Fear). In this short book, Han observes that hope is always associated with a „we“ and an „us“. We hope for example, that things will work out right in the end and we hope that nature will give us a second chance. This is diametrically opposed to the alienated culture of fear that is the hall-mark of contemporary culture. Han also observes that historically, modernism was always concerned with leaving the past behind and setting out in search of something new. This is diametrically opposed to contemporary art where again there is no vision and no intention of leaving the confines of the present or of the status quo that is destroying our environmental niche.

On Thursday, 49 copies of The Venus of Willendorf and the Culture of the Gravette are delivered to my door whilst on Friday, I measure the Museum Krems sculpture of Saint Vitus in a Vat and am at last able to confirm that the legs of the cauldron in which the Saint is being boiled, do indeed mark out a 13, 14, 15 triangle. This occurs repeatedly in Piero della Francesca’s Libellus de cinque corpi regularibus. This is hugely important as two forthcoming books and an article have for several years rested on a hypothesis confirmed by nothing more than rule of thumb observations made without removing the work from its display case.
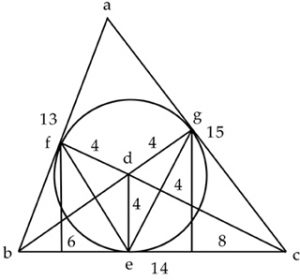
The matter confirmed, publication in 2025 of the books can go ahead as planned whilst the article requires some additional work but will hopefully be out soon.

Week 48
My thesis on the sculpture of Saint Vitus in a Vat confirmed, I set about summarising the theory in an explanatory diagram and incorporating the results into the next two forthcoming Reloading Humanism Guides.
While I enjoy reading Robert Macfarlane’s Old Ways, it is very much a modernist cup of tea and the bottom line is „I’ll take you to water but I won’t let you drink“. This is the unwritten credo of modern culture. For our mental and emotional well-being we hanker after something which in older cultures was supplied by a shared set of beliefs. In modern culture, instead of being given what we yearn for or being told how we might arrive at it, we are told why we can’t have it and that wanting it is in any case old fashioned and out of date. While we yearn for such things as spiritual orientation and beauty, our culture fails to provide it. In his book, Macfarlane visits the sculptor, Steve Dilworth, who lives on the Isle of Harris and the theme is continued. Some of Dilworth’s pieces I find intriguing, others are repellent, including The Hanging Figure, which is made from human bones tied together with grass and horsehair and which was then filed out with the organs of a calf. For an image and an introduction to Dilworth’s work see: https://.geoginacoburnarts.co.uk.
This can betaken as an image of what modernism tells who we are and it is easy to see that only curators and self-appointed experts will argue that it is beautiful and inspiring. All this is deeply hypocritical as instead of seeing ourselves as a part of evolution, we see ourselves as unwanted orphans who have been deliberately cast out and abandoned in a wood. This is however is a romantic notion if ever there was and therefore something which „Oh so clever“ modernists should be above. But they are not and instead, with their pseudo-intellectualism, invite us to wallow in an uncritically accepted fantasy. That is infantile, irresponsible, narcissistic and nauseatingly self-staged. Nevertheless we accept this as it allows us to con ourselves into thinking that we don’t have to do anything about the state of the world, there is no point caring about what sort of world our children will inherit and that we are in no way behoven take a deep hard look at ourselves and what we are up to.
Reloading Humanism is a reaction against all this and is about providing a properly thought-out philosophy with a responsible and dignified image of who we are and what it is that we are supposed to do. To this effect I must resurrect Plato, Parmenides and the Renaissance and show how, repeatedly in the past, people saw the world as being beautiful, complex and sophisticated, with all things being bound back on themselves to result in self-regulating systems. Then, combining art, mathematics and philosophy, I must work out something appropriate to the here and now of our own age.
Week 49

In the Krems Town Archive, I trawl through books of protocols, looking at the inventories periodically drawn up of everything that the Burgesses‘ Hospice in Krems owned. Although it is assumed and indeed is logical that it was the Burgesses‘ Hospice that commissioned and owned the sculpture of Saint Vitus in a Vat, there is no written evidence confirming this. By systematically looking through the inventories, the hope is that I might stumble on a mention of the Saint in a Vat but no, there is nothing. The closest I come is an entry of „a three legged stand for boiling water for which the cauldron is missing“. Working my way through the ledgers, I find that works of art are not described at all but are simply mentioned as „a picture“, „a crucifix“. Whilst not helpful, this at least provides some explanation of why, in the records, the Saint should be so consistently elusive.

Unlike Italian Renaissance writing which was modelled on Roman letters, sixteenth century German handwriting remains true to the Gothic style and is flowery and difficult to read. Nevertheless, titles are easy enough and a name catches my eye. This is the heading of a will drawn up by Adam Händl who taught Latin in Krems and who was the director of the church choir. Accordingly, he must have owned books and apart from looking for references to Saint Vitus, I am also on the lookout for mentions of books. Adam Händl is on my radar as he composed a piece of music for four voices, the score of which I photographed in the National Library in Vienna and which may feature on a music CD that I have plans for. Wrestling with the clerk’s writing I am delighted to see that, as mentioned in his will of 1568 on Folio 108v, Adam Händl was the owner of books on philosophy. Unfortunately this is as far as the will goes and individual titles, although often given, are in this case not listed.
Week 50
My work in the Town Archive finished, I begin work on the layout of Rediscovering History in Krems and the Wachau. Searching out and preparing a hundred-odd images, I insert them into the text. Yet numerous images are missing and as I slowly fill in the missing gaps, I find that as author, graphic artist and illustrator, I can adapt and change elements in ways that are normally not possible. Not only can I change images to suit spaces in the text, I can rewrite texts so as to make blocks of text longer or shorter and can chose between inserting information in the text or, using smaller letters, in the place reserved for picture captions. In this way, the layout process becomes a form of second edit, in which seeing things anew, I am repeatedly prompted to check and re-check not only entries and information but also that everything that needs to be explained, not only is explained but is done so in the right way and at the right place and without unnecessary repetition.

As the day of the winter solstice slowly approaches I realise how, on my console table, the discrepancy between the day of the solstice and the date of Christmas is to be resolved. In The Bible it says that Christ is the Light of the World and this suggests that he is to be associated with the sun and to accordingly have his birthday on the day of the winter solstice. Yet The Bible it also says that the presentation at the Temple was exactly 40 days after Christmas and as explained in January, the festival of Imbolc , which was Christianised to become Candlemass, was a festival of such importance that could not be moved forward. Thus Christmas Day is celebrated four days after the winter solstice. On the table, the resolution of this tension is to replace the November hourglass of All Souls, with the Yule Log of Christmas. Then on Christmas Day, the log is to be burnt and the ashes placed in a glass jar on the table for the duration of the Christmas period. As in times of old, when the Twelve Days of Christmas are over, the ashes are to be scattered in the garden to help ensure a good gardening year and fertility for 2025.
Week 51

Replacing the hourglass on my console table, with the Yule Log, the significance of what I am doing suddenly becomes clear. As argued in Rediscovering History, for thousands of years, time, the year and the cycles of the seasons were envisaged as a snake or dragon who was seen as The Great Goddess of All Things. Although in this aspect a dragon, the goddess could metamorphose and in human form was imagined as a woman who in spring was a maiden, in summer was a mature woman, whilst in the autumn she became an old hag. This raises the question of, „What form does she take during the winter and how is this three-folded nature to be brought in tune with the four seasons which make up the year?“ Prompted by my console table, I have the answer. After scattering the ashes of the Yule Log in the garden, all I have to do is to return the empty jar to the table and leave it there until the beginning of February. This means that on the day of the winter solstice, the goddess dies and disappears. The fourth season is thus an empty season, a non-season when everything in nature is frozen and dead.
Seen from the Schreckberg above Stein, on the day of the summer solstice, the sun rises over a plateaux at a point below which, there is a gully whose meandering forms point towards the Schreckberg. This and the fact that the gully is called „Wolfsgraben“, I know from a map. In Rediscovering History I mention these facts and allude to them in the chapter’s title. The problem is that the structure of the book means that there must be something at Wolfsgraben that is relevant to the contents of the chapter and which is also worth seeing. Not knowing what (if anything) awaits me, the day after the solstice, I set off to find out. As expected, the gully is mostly overgrown, with young trees growing on abandoned terraces where once vines were grown. Along the way, I pass dilapidated wine cellars which whilst suitably intriguing, are not appropriate enough. Climbing higher, there are some cultivated terraces but not many. After a while, to get back in line with the direction of the Schreckberg, I turn right and follow a path up towards the plateaux. At the top, I see the concrete roof of a wine cellar that was built in the 1950’ies or 1960’ies. Approaching, I make out the forms of a huge single bladed plough and immediately know that this is what I need. Appropriately it looks like a cubist sculpture of a dying dragon and I can’t help seeing it as a sign confirming my hypothesis as to how the three-folded nature of The Great Goddess of the Neolithic is to be squared with the four-folded nature of the cycle of the seasons.

Week 52
Going hand in hand with these revelations and insights, over the weeks I have been making copies of a number of sculptures and artefacts that I need to photograph for Rediscovering History. While this is necessary in order to avoid copyright issues, the process of making copies is not only instructive but also brings new insights. Appropriately, two images show The Great Goddess of the Neolithic. Where the first shows her as a bird-woman:

the second shows her as a maiden, plaintively invoking the sky to shower her with rain:

The second is the most bizarre image from prehistory that I have encountered and shows the goddess as a toad and as a woman with a clearly non-human face.

Unknown outside archaeological circles the image includes a highly detailed rendition of female genitalia. See, with a 3-D virtual model being available at: https://uhasammlung.univie.ac.at
Although known as the „Lady Toad of Maissau“, the image is a three-fold composite and is possibly a toad/woman/sow. Usually shown in the form of plan views, either from above and below, or with only the lower side being shown, in the archaeological write-up, it is suggested that the lower side represents a woman during a moment of intimacy. With the finished copy in my hands however, I am free to move it about as I wish. Looking at it from all angles, in the light of my insights concerning the seasons, I see the image as going beyond this to become a highly charged invocation to The Great Goddess of the Neolithic to inaugurate the beginnings of spring. Flying through the air, she brings life, desire and fertility where ever she goes. This augments the purely erotic interpretation and shows how taking a holistic approach can provide richer understanding.

Although I love the buzz and frenzy of Christmas, I know that behind the excitement of celebrating with family and friends, there must also be moments of withdrawal and regeneration and with this very much in mind, I have a peaceful Christmas and in a silent ceremony, the Yule Log is burnt with only the single eye of a camera as an onlooker other than myself.

Incorporating the above insights into my book, I realise that although The Great Goddess of the Neolithic dies on the day of the winter solstice, she does not immediately disappear but instead, as recorded in Austrian folk lore, rampages by night as a ghost over hill and dale, accompanied by a terrifying following of grisly characters. This is the „Wild Hunt“, which in Austria is associated with the time between the winter solstice and 6th January. During this time the goddess, who usually encourages industry, punishes those work and fail to obey the holiday. Subtracting the days between the winter solstice and Christmas Day, from the days and nights of the Raunachten, gives twelve, resulting in the Twelve Days of Christmas.

